
分析 (Ⅰ)由$\sqrt{3}$a=2bsinA,利用正弦定理得$\sqrt{3}$sinA=2sinBsinA,从而可得sinB=$\frac{\sqrt{3}}{2}$,结合0<B<π,且a<b<c,可求B.
(Ⅱ)利用余弦定理即可解得c的值.
解答 解:(Ⅰ)由$\sqrt{3}$a=2bsinA,得$\sqrt{3}$sinA=2sinBsinA,
因为0<A<π,所以sinA≠0,
所以sinB=$\frac{\sqrt{3}}{2}$,
因为0<B<π,且a<b<c,
所以B=60°.
(Ⅱ)因为B=60°,a=2,$b=\sqrt{7}$,
所以,由余弦定理可得:b2=a2+c2-2accosB,即:7=4+c2-2×$2×c×\frac{1}{2}$,整理可得:c2-2c-3=0,
所以解得:c=3或-1(舍去).
点评 本题考查正弦定理、余弦定理的运用,考查学生的数形结合思想和计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-{y^2}=1$ | B. | ${x^2}-\frac{y^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{2}-{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{9}{10},\;4]$ | B. | $[\frac{{3\sqrt{10}}}{10},\;2]$ | C. | [1,2] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
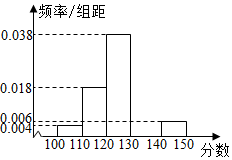 2015-2016学年高二A班50名学生在其中数学测试中(满分150分),成绩都介于100分到150分之间,将测试结果按如下方式分成五组,第一组[100,110),第二组[110,120),…,第五组[140,150),按上述分组方法得到的频率分布直方图如图所示,
2015-2016学年高二A班50名学生在其中数学测试中(满分150分),成绩都介于100分到150分之间,将测试结果按如下方式分成五组,第一组[100,110),第二组[110,120),…,第五组[140,150),按上述分组方法得到的频率分布直方图如图所示,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com