解:(1)∵锐角B满足
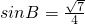
,∴cosB=

.
∴
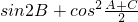
=2sinBcosB+
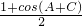
=
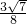
+
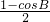
=
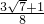
.
(2)由余弦定理可得 b
2=2=a
2+c
2-2accosB≥2ac-2ac×

,
解得ac≤4,当且仅当a=c=2时,等号成立,故此时△ABC的面积为

=

.
分析:(1)由锐角B满足
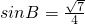
,求得cosB 的值,再利用二倍角公式化简要求的式子为2sinBcosB+
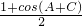
,运算求得结果.
(2)由余弦定理可得 b
2=2=a
2+c
2-2accosB,再由基本不等式求得ac≤4,当且仅当a=c=2,由此求得△ABC的面积.
点评:本题主要考查余弦定理,同角三角函数的基本关系,诱导公式以及二倍角公式、基本不等式的应用,属于中档题..

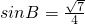 .
.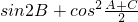 的值.
的值.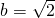 ,当ac取最大值时,求△ABC的面积.
,当ac取最大值时,求△ABC的面积.