
【题目】在平面直角坐标系中,O为坐标原点,已知向量 ![]() =(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t).
=(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t).
(1)若 ![]() ⊥
⊥ ![]() ,且|
,且| ![]() |=
|= ![]() |
| ![]() |,求向量
|,求向量 ![]() ;
;
(2)若向量 ![]() 与向量
与向量 ![]() 共线,常数k>0,求f(θ)=tsinθ的值域;
共线,常数k>0,求f(θ)=tsinθ的值域;
(3)当(2)问中f(θ)的最大值4时,求 ![]()
![]() .
.
【答案】
(1)解: ![]() ,∵
,∵ ![]() ,
,
∴8﹣n+2t=0
又 ![]() ,∴(n﹣8)2+t2=5×64得t=±8,
,∴(n﹣8)2+t2=5×64得t=±8,
∴ ![]() 或(﹣8,﹣8)
或(﹣8,﹣8)
(2)解: ![]() ,
,
∵向量 ![]() 与向量
与向量 ![]() 共线,
共线,
∴t=﹣2ksinθ+16,f(θ)=tsinθ=(﹣2ksinθ+16)sinθ= ![]()
① ![]() ,∴
,∴ ![]() 时,f(θ)=tsinθ取最大值为
时,f(θ)=tsinθ取最大值为 ![]() ,
,
sinθ=﹣1时,f(θ)取得最小值为﹣2k﹣16,
此时函数的值域为[﹣2k﹣16, ![]() ]
]
② ![]() ,
,
∴sinθ=1时,tsinθ取最大值为﹣2k+16,
sinθ=﹣1时,f(θ)取得最小值为﹣2k﹣16,
此时函数的值域为[﹣2k﹣16,﹣2k+16].
(3)解:①当k>4时,由 ![]() =4,得k=8,此时
=4,得k=8,此时 ![]() ,
, ![]() ,
,
∴ ![]()
②当0<k<4时,由﹣2k+16=4,得k=6,(舍去)
综上所述,∴ ![]() =32
=32
【解析】(1)利用向量垂直的坐标表示及向量模的坐标表示,列出关于n,t的方程组,并解即可.(2)向量 ![]() 与向量
与向量 ![]() 共线,得出f(θ)=tsinθ=(﹣2ksinθ+16)sinθ,利用配方法结合一元二次函数的最值性质进行求解.(3)根据(2)问中f(θ)的最大值4时,建立方程关系求出k或θ,求
共线,得出f(θ)=tsinθ=(﹣2ksinθ+16)sinθ,利用配方法结合一元二次函数的最值性质进行求解.(3)根据(2)问中f(θ)的最大值4时,建立方程关系求出k或θ,求 ![]() 即可.
即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两名同学8次数学测验成绩如茎叶图所示, ![]() 1 ,
1 , ![]() 2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1 , s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )
2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1 , s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )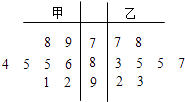
A.![]() 1>
1> ![]() 2 , s1<s2
2 , s1<s2![]()
B.![]() 1=
1= ![]() 2 , s1<s2
2 , s1<s2![]()
C.![]() 1=
1= ![]() 2 , s1=s2
2 , s1=s2 ![]()
D.![]() 1<
1< ![]() 2 , s1>s2
2 , s1>s2![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )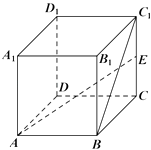
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差为0的等差数列{an}满足a1=1,且a1 , a3﹣2,a9成等比数列.
(1)求数列{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 并求使得Sn>
}的前n项和为Sn , 并求使得Sn> ![]() +
+ ![]() 成立的最小正整数n.
成立的最小正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=﹣ ![]() ,Sn+
,Sn+ ![]() =an﹣2(n≥2,n∈N)
=an﹣2(n≥2,n∈N)
(1)求S2 , S3 , S4的值;
(2)猜想Sn的表达式;并用数学归纳法加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com