
【题目】已知公差为0的等差数列{an}满足a1=1,且a1 , a3﹣2,a9成等比数列.
(1)求数列{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 并求使得Sn>
}的前n项和为Sn , 并求使得Sn> ![]() +
+ ![]() 成立的最小正整数n.
成立的最小正整数n.
【答案】
(1)解:设数列{an}的公差为d,
由a1,a3﹣2,a9成等比数列得,(2d﹣1)2=1×(1+8d),
则d2﹣3d=0,解得d=3或d=0(舍去),
所以an=1+(n﹣1)d=3n﹣2;
(2)解:由(1)得, ![]() =
= ![]() =
= ![]() (
( ![]() ),
),
则Sn= ![]() [(1﹣
[(1﹣ ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )]
)]
= ![]() (
( ![]() )=
)= ![]() ,
,
所以Sn> ![]() +
+ ![]() 为
为 ![]() >
> ![]() +
+ ![]() ,化简得,
,化简得,
n2﹣25n﹣8>0,又n是正整数,解得n≥26,
所以Sn= ![]() ,使得Sn>
,使得Sn> ![]() +
+ ![]() 成立的最小正整数n为26
成立的最小正整数n为26
【解析】(1)设数列{an}的公差为d,根据等比中项的性质、等差数列的通项公式列出方程,求出d的值,代入等差数列的通项公式求出an;(2)由(1)化简 ![]() ,利用裂项相消法求出Sn , 化简Sn>
,利用裂项相消法求出Sn , 化简Sn> ![]() +
+ ![]() 求出n的范围,即可求出最小正整数n.
求出n的范围,即可求出最小正整数n.
【考点精析】通过灵活运用等差数列的通项公式(及其变式)和数列的前n项和,掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系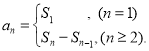 即可以解答此题.
即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x+2y+m=0与y轴交于A,B两点,且∠ACB=90°(C为圆心),过点P(0,2)且斜率为k的直线与圆C相交于M,N两点.
(1)求实数m的值;
(2)若|MN|≥4,求k的取值范围;
(3)若向量 ![]() 与向量
与向量 ![]() 共线(O为坐标原点),求k的值.
共线(O为坐标原点),求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,已知向量 ![]() =(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t).
=(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t).
(1)若 ![]() ⊥
⊥ ![]() ,且|
,且| ![]() |=
|= ![]() |
| ![]() |,求向量
|,求向量 ![]() ;
;
(2)若向量 ![]() 与向量
与向量 ![]() 共线,常数k>0,求f(θ)=tsinθ的值域;
共线,常数k>0,求f(θ)=tsinθ的值域;
(3)当(2)问中f(θ)的最大值4时,求 ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,在以极点为直角坐标原点
,在以极点为直角坐标原点![]() ,极轴为
,极轴为![]() 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为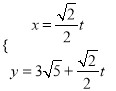 (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,设曲线![]() 经过伸缩变换
经过伸缩变换![]() :
: 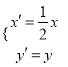 得到曲线
得到曲线![]() ,若
,若![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点. 
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位举行联欢活动,每名职工均有一次抽奖机会,每次抽奖都是从甲箱和乙箱中各随机摸取1个球,已知甲箱中装有3个红球,5个绿球,乙箱中装有3个红球,3个绿球,2个黄球.在摸出的2个球中,若都是红球,则获得一等奖;若都是绿球,则获得二等奖;若只有1个红球,则获得三等奖;若1个绿球和1个黄球,则不获奖.
(1)求每名职工获奖的概率;
(2)设X为前3名职工抽奖中获得一等奖和二等奖的次数之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比为正整数的等比数列,{bn}是等差数列,且a1a2a3=64,b1+b2+b3=﹣42,6a1+b1=2a3+b3=0.
(1)求数列{an}和{bn}的通项公式;
(2)设pn= ![]() ,数列{pn}的前n项和为Sn .
,数列{pn}的前n项和为Sn .
①试求最小的正整数n0 , 使得当n≥n0时,都有S2n>0成立;
②是否存在正整数m,n(m<n),使得Sm=Sn成立?若存在,请求出所有满足条件的m,n;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com