
【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点. 
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值.
【答案】
(1)证明:连接A1C,交AC1于点E,
则点E是A1C及AC1的中点.
连接DE,则DE∥A1B.
因为DE平面ADC1,
所以A1B∥平面ADC1.
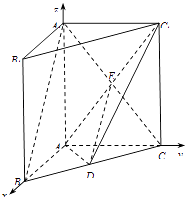
(2)解:建立如图所示空间直角坐标系A﹣xyz.
则A(0,0,0),B(1,0,0),C(0,1,0),
C1(0,1,2)D( ![]() ,
, ![]() ,0),
,0),
![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(0,1,2).
=(0,1,2).
设平面ADC1的法向量 ![]() =(x,y,z),
=(x,y,z),
则 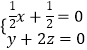 ,不妨取
,不妨取 ![]() =(2,﹣2,1).
=(2,﹣2,1).
平面ABA1的一个法向量 ![]() =
= ![]() =(0,1,0).
=(0,1,0).
|cos< ![]() ,
, ![]() >|=|
>|=| ![]() |=
|= ![]() ,
,
设平面ADC1与ABA1所成二面角的平面角为θ,
sinθ= ![]() =
= ![]() .
.
∴平面ADC1与ABA1所成二面角的正弦值是 ![]() .
.
【解析】(1)连接A1C,交AC1于点E,连接DE,则DE∥A1B,由此能证明A1B∥平面ADC1 . (2)建立空间直角坐标系A﹣xyz.利用向量法能求出平面ADC1与ABA1所成二面角的正弦值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )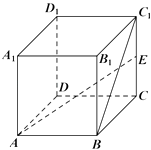
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是偶函数,且f(x+ ![]() )=f(
)=f( ![]() ﹣x),当﹣
﹣x),当﹣ ![]() ≤x≤0时,f(x)=(
≤x≤0时,f(x)=( ![]() )x﹣1,记an=f(
)x﹣1,记an=f( ![]() ),n∈N+ , 则a2046的值为( )
),n∈N+ , 则a2046的值为( )
A.1﹣ ![]()
B.1﹣ ![]()
C.![]() ﹣1
﹣1![]()
D.![]() ﹣1
﹣1![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差为0的等差数列{an}满足a1=1,且a1 , a3﹣2,a9成等比数列.
(1)求数列{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 并求使得Sn>
}的前n项和为Sn , 并求使得Sn> ![]() +
+ ![]() 成立的最小正整数n.
成立的最小正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , 对于实数m、n、p有f(m+n)=f(m)+f(n),f(m+n+p)=f(m)+f(n)+f(p),则p的最大值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系,长郡中学数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占![]() ,统计成绩后,得到如下的
,统计成绩后,得到如下的![]() 列联表:
列联表:
分数大于等于120分 | 分数不足120分 | 合计 | |
周做题时间不少于15小时 | 4 | 19 | |
周做题时间不足15小时 | |||
合计 | 45 |
(1)请完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
(2)(ⅰ)按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
(ⅱ)若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
|
|
|
|
|
|
|
|
附: 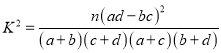
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com