
已知数列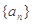 的前
的前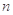 项和为
项和为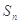 ,数列
,数列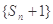 是公比为
是公比为 的等比数列,
的等比数列,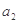 是
是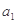 和
和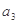 的等比中项.
的等比中项.
(1)求数列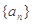 的通项公式;
的通项公式;
(2)求数列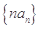 的前
的前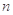 项和
项和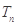 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知数列{an}的前n项和为Sn,且Sn=2an-2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn=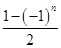 an-
an-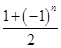 bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为保护我国的稀土资源,国家限定某矿区的出口总量不能超过80吨,该矿区计划从2006年开始出口,当年出口a吨,以后每一年出口量均比上一年减少10%.
(Ⅰ)以2006年为第一年,设第n年出口量为an吨,试求an.
(Ⅱ)因稀土资源不能再生,国家计划10年后终止该矿区的出口,问2006年最多出口多少吨?(保留一位小数)参考数据:0.910≈0.35.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com