
已知数列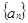 的前
的前 项和
项和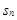 满足
满足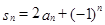 ,
,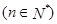
(Ⅰ)求数列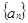 的前三项
的前三项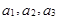
(Ⅱ)设 ,求证:数列
,求证:数列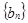 为等比数列,并指出
为等比数列,并指出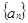 的通项公式。
的通项公式。
(Ⅰ) 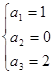 ;(Ⅱ)
;(Ⅱ)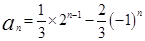 .
.
解析试题分析:(Ⅰ) 求数列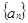 的前三项
的前三项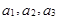 ,在
,在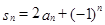 中分别令
中分别令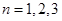 即可求出
即可求出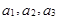 ;(Ⅱ)数列
;(Ⅱ)数列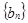 为等比数列,只需证明
为等比数列,只需证明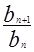 等于一个与
等于一个与 无关的常数,由
无关的常数,由 ,首先求出数列
,首先求出数列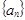 的通项公式,或递推式,由
的通项公式,或递推式,由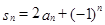 ,这是已知
,这是已知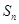 ,求
,求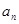 ,可利用
,可利用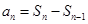 来求,即当
来求,即当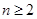 ,
,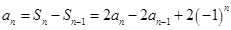 ,可得
,可得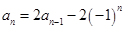 ,由
,由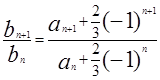 ,把
,把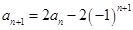 代入可得
代入可得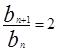 ,从而可证,求
,从而可证,求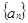 的通项公式,由
的通项公式,由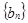 是首项为
是首项为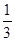 ,公比为2的等比数列,可写出
,公比为2的等比数列,可写出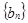 的通项公式,从而可得数列
的通项公式,从而可得数列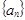 的通项公式.
的通项公式.
试题解析:(Ⅰ)在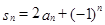 中分别令n=1,2,3得
中分别令n=1,2,3得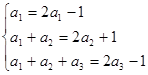 (2分) 解得
(2分) 解得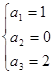 (4分)
(4分)
⑵由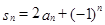 ,n≥1得
,n≥1得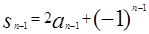 ,n≥2
,n≥2
两式想减得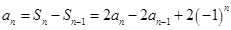 ,即
,即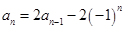 , (6分)
, (6分)
∴an+ (-1)n=2an-1+
(-1)n=2an-1+ (-1)n-2(-1)n=2an-1+
(-1)n-2(-1)n=2an-1+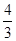 (-1)n-1
(-1)n-1
=2[an-1+ (-1)n-1](n≥2) (9分)
(-1)n-1](n≥2) (9分)
即bn=2bn-1(n≥2),b1=a1- =
=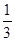
∴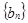 是首项为
是首项为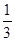 ,公比为2的等比数列. (10分)
,公比为2的等比数列. (10分)
∴bn=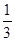 ×2n-1= an+
×2n-1= an+ (-1)n
(-1)n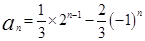 (12分)
(12分)
考点:等比数列的判断,求通项公式.


科目:高中数学 来源: 题型:填空题
设a1,a2, ,an为正整数,其中至少有五个不同值. 若对于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,则n的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列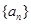 的前
的前 项和
项和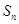 和通项
和通项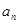 满足
满足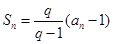 (
(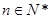 ,
,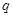 是大于0的常数,且
是大于0的常数,且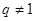 ),数列
),数列 是公比不为
是公比不为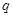 的等比数列,
的等比数列,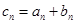 .
.
(1)求数列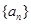 的通项公式;
的通项公式;
(2)设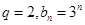 ,是否存在实数
,是否存在实数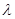 ,使数列
,使数列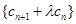 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数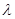 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)数列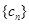 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的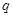 和
和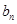 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(文)对于数列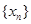 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为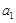 ,公差为
,公差为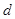 的无穷等差数列
的无穷等差数列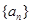 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项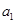 ,第三项
,第三项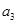 和第五项
和第五项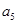 .
.
(1) 若 成等比数列,求
成等比数列,求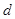 的值;
的值;
(2) 在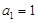 ,
, 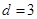 的无穷等差数列
的无穷等差数列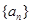 中,是否存在无穷子数列
中,是否存在无穷子数列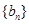 ,使得数列
,使得数列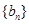 为等比数列?若存在,请给出数列
为等比数列?若存在,请给出数列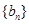 的通项公式并证明;若不存在,说明理由;
的通项公式并证明;若不存在,说明理由;
(3) 他在研究过程中猜想了一个命题:“对于首项为正整数 ,公比为正整数
,公比为正整数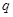 (
(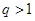 )的无穷等比数 列
)的无穷等比数 列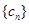 ,总可以找到一个子数列
,总可以找到一个子数列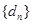 ,使得
,使得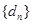 构成等差数列”. 于是,他在数列
构成等差数列”. 于是,他在数列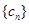 中任取三项
中任取三项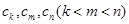 ,由
,由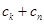 与
与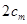 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对于数列 ,
,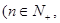
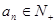 ),若
),若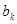 为
为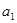 ,
,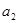 ,….,
,….,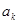 中最大值(
中最大值(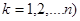 ,则称数列
,则称数列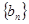 为数列
为数列 的“凸值数列”。如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有______
的“凸值数列”。如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有______
①递减数列 的“凸值数列”是常数列;②不存在数列
的“凸值数列”是常数列;②不存在数列 ,它的“凸值数列”还是
,它的“凸值数列”还是 本身;
本身;
③任意数列 的“凸值数列”递增数列;④“凸值数列”为1,3,3,9,的所有数列
的“凸值数列”递增数列;④“凸值数列”为1,3,3,9,的所有数列 的个数为3.
的个数为3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com