
设a1,a2, ,an为正整数,其中至少有五个不同值. 若对于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,则n的最小值是 .
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:填空题
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数. 他们研究过如图所示的三角形数: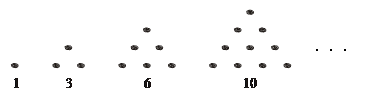
|
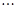 记为数列
记为数列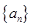 ,将可被5整除的三角形数按从小到大的顺序组成一个新数列
,将可被5整除的三角形数按从小到大的顺序组成一个新数列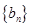 . 可以推测:(Ⅰ)
. 可以推测:(Ⅰ)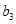 是数列
是数列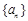 中的第 项;
中的第 项;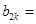 ________(用k表示)
________(用k表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com