练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O是底面中心，A1O⊥底面ABCD，AB＝AA1＝.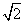

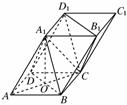
     (1)证明：平面A1BD∥平面CD1B1；

    (2)求三棱柱ABD－A1B1D1的体积．


    　(1)证明：由题设知，BB1綊DD1，

    ∴四边形BB1D1D是平行四边形，∴BD∥B1D1.

    又BD⃘平面CD1B1，∴BD∥平面CD1B1.

    ∵A1D1綊B1C1綊BC，∴四边形A1BCD1是平行四边形，

    ∴A1B∥D1C.

    又A1B⊄平面CD1B1，∴A1B∥平面CD1B1.

    又BD∩A1B＝B，∴平面A1BD∥平面CD1B1.

    (2)∵A1O⊥平面ABCD，

    ∴A1O是三棱柱ABD－A1B1D1的高．

    又AO＝AC＝1，AA1＝，∴A1O＝＝1.

    又S△ABD＝＝1，

    ∴V三棱柱ABD－A1B1D1＝S△ABD·A1O＝1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知全集U＝(－∞，3]，A＝[－1，2)，则∁UA＝____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有编号为1,2,3的三个白球，编号为4,5,6的三个黑球，这六个球除编号和颜色外完全相同，现从中任意取出两个球．

    (1)求取得的两个球颜色相同的概率；

    (2)求取得的两个球颜色不相同的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设关于x，y的不等式组表示的平面区域内存在点P(x0，y0)，满足x0－2y0＝2.求得m的取值范围是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|x－a|.

    (1)若不等式f(x)≤3的解集为{x|－1≤x≤5}，求实数a的值；

    (2)在(1)的条件下，若f(x)＋f(x＋5)≥m对一切实数x恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)

    A．α∥β且l∥α

    B．α⊥β且l⊥β

    C．α与β相交，且交线垂直于l

    D．α与β相交，且交线平行于l

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，正方体ABCD－A1B1C1D1的棱长为1，点M∈AB1，N∈BC1，且AM＝BN≠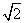，有以下四个结论：

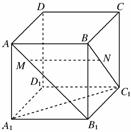
    ①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1是异面直线．其中正确命题的序号是________．(注：把你认为正确命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝|x2－a|在区间[－1,1]上的最大值M(a)的最小值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列为等差数列，且

       （Ⅰ）求数列的通项公式；  

    （Ⅱ）证明：。

    查看答案和解析>>

    同步练习册答案