
有编号为1,2,3的三个白球,编号为4,5,6的三个黑球,这六个球除编号和颜色外完全相同,现从中任意取出两个球.
(1)求取得的两个球颜色相同的概率;
(2)求取得的两个球颜色不相同的概率.
解析: 从六个球中取出两个球的基本事件:
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共计15个基本事件.
(1)记事件A为取出的两个球是白球,则这个事件包含的基本事件是(1,2),(1,3),(2,3),共计3个基本事件,故P(A)=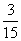 =
=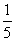 .
.
记取出的两个球是黑球为事件B,同理可得P(B)=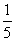 .
.
记事件C为取出的两个球的颜色相同,则C=A+B,且A,B互斥,根据互斥事件的概率加法公式,得P(C)=P(A+B)=P(A)+P(B)=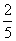 .
.
(2)记事件D为取出的两个球的颜色不相同,则事件C,D互斥,根据互斥事件概率之间的关系,得P(D)=1-P(C)=1-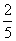 =
=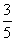 .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
已知集合A={x|ax2-3x+2=0,a∈R}.
(1) 若A是空集,求a的取值范围;
(2) 若A中只有一个元素,求a的值,并将这个元素写出来;
(3) 若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中的真命题有________.(填序号)
① x∈R,x+
x∈R,x+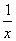 =2;
=2;
②  x∈R,sinx=-1;
x∈R,sinx=-1;
③  x∈R,x2>0;
x∈R,x2>0;
④  x∈R,2x>0.
x∈R,2x>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}、{bn}、{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),求证:{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn+1(n=1,2,3,…).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C的中心在坐标原点,焦点在x轴上且过点P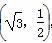 ,离心率是
,离心率是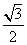 .
.
(1)求椭圆C的标准方程;
(2)直线l过点E (-1,0)且与椭圆C交于A,B两点,若|EA|=2|EB|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=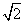 .
.
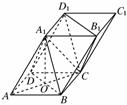
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com