
设数列{an}、{bn}、{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),求证:{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn+1(n=1,2,3,…).
证明:必要性:
设{an}是公差为d1的等差数列,则
bn+1-bn=(an+1-an+3) - (an-an+2)
= (an+1-an) - (an+3-an+2)= d1- d1=0,
所以bn≤bn+1(n=1,2,3,…)成立.
又cn+1-cn=(an+1-an)+2(an+2-an+1)+3(an+3-an+2)= d1+2d1 +3d1 =6d1(常数)(n=1,2,3,…),
所以数列{cn}为等差数列.
充分性:
设数列{cn}是公差为d2的等差数列,且bn≤bn+1(n=1,2,3,…).
∵ cn=an+2an+1+3an+2, ①
∴ cn+2=an+2+2an+3+3an+4, ②
①-②,得cn-cn+2=(an-an+2)+2 (an+1-an+3)+3 (an+2-an+4)=bn+2bn+1+3bn+2.
∵ cn-cn+2=(cn-cn+1)+(cn+1-cn+2)= -2d2,
∴ bn+2bn+1+3bn+2=-2d2, ③
从而有bn+1+2bn+2+3bn+3=-2d2, ④
④-③,得(bn+1-bn)+2 (bn+2-bn+1)+3 (bn+3-bn+2)=0.⑤
∵ bn+1-bn≥0,bn+2-bn+1≥0,bn+3-bn+2≥0,
∴ 由⑤得bn+1-bn=0(n=1,2,3,…).
由此不妨设bn=d3 (n=1,2,3,…),则an-an+2=d3(常数).
由此cn=an+2an+1+3an+2cn=4an+2an+1-3d3,
从而cn+1=4an+1+2an+2-5d3,
两式相减得cn+1-cn=2(an+1-an) -2d3,
因此an+1-an=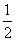 (cn+1-cn)+d3=
(cn+1-cn)+d3=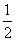 d2+d3(常数) (n=1,2,3,…),
d2+d3(常数) (n=1,2,3,…),
∴ 数列{an}为等差数列.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
已知数列{an}的各项都为正数,且对任意n∈N*,a2n-1,a2n,a2n+1成等差数列,
a2n,a2n+1,a2n+2成等比数列.
(1)若a2=1,a5=3,求a1的值;
(2)设a1<a2,求证:对任意n∈N*,且n≥2,都有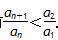
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个结论正确的是________.(填序号)
① “x≠0”是“x+|x|>0”的必要不充分条件;
② 已知a、b∈R,则“|a+b|=|a|+|b|”的充要条件是ab>0;
③ “a>0,且Δ=b2-4ac≤0”是“一元二次不等式ax2+bx+c≥0的解集是R”的充要条件;
④ “x≠1”是“x2≠1”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
有编号为1,2,3的三个白球,编号为4,5,6的三个黑球,这六个球除编号和颜色外完全相同,现从中任意取出两个球.
(1)求取得的两个球颜色相同的概率;
(2)求取得的两个球颜色不相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com