
已知向量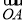 =(3,-4),
=(3,-4),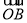 =(6,-3),
=(6,-3),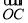 =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A,B,C不能构成三角形,求实数m满足的条件;
若△ABC为直角三角形,求实数m的值.
(1)m=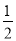 ;(2)m=
;(2)m=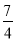 或-
或-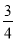 或
或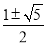 .
.
【解析】
试题分析:(1)利用向量的运算法则求出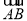 ,
,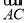 ;利用向量垂直的充要条件列出方程求出m.
;利用向量垂直的充要条件列出方程求出m.
(2)将构成三角形转化为三点不共线,,将几何中的角为直角转化为向量的语言,通过向量的数量积为零列出关于实数m的方程,求解出实数m.
(1)∵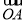 =(3,-4),
=(3,-4),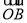 =(6,-3),
=(6,-3),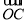 =(5-m,-3-m),若A,B,C三点不能构成三角形,则这三点共线,∵
=(5-m,-3-m),若A,B,C三点不能构成三角形,则这三点共线,∵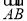 =(3,1),
=(3,1),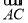 =(2-m,1-m),∴3(1-m)=2-m,∴m=
=(2-m,1-m),∴3(1-m)=2-m,∴m=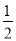 即为满足的条件.(2)由题意,△ABC为直角三角形,①若∠A=90°,则
即为满足的条件.(2)由题意,△ABC为直角三角形,①若∠A=90°,则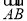 ⊥
⊥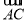 ,∴3(2-m)+(1-m)=0,∴m=
,∴3(2-m)+(1-m)=0,∴m=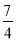 .②若∠B=90°,则
.②若∠B=90°,则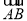 ⊥
⊥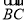 ,∵
,∵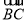 (-1-m,-m),∴3(-1-m)+(-m)=0,∴m=-
(-1-m,-m),∴3(-1-m)+(-m)=0,∴m=-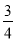 . ③若∠C=90°,则
. ③若∠C=90°,则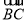 ⊥
⊥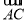 , ∴(2-m)(-1-m)+(1-m)(-m)=0,∴m=
, ∴(2-m)(-1-m)+(1-m)(-m)=0,∴m=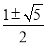 .综上可得,m=
.综上可得,m=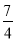 或-
或-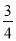 或
或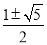 .
.
考点:平面向量共线(平行)的坐标表示;数量积判断两个平面向量的垂直关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016届广东省高一下学期第一次阶段考试数学试卷(解析版) 题型:选择题
圆锥的表面积是底面积的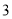 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )
A.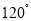 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期期中数学试卷(解析版) 题型:选择题
已知函数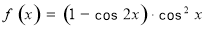 ,
, R,则f(x)是( )
R,则f(x)是( )
A.最小正周期为 的奇函数
的奇函数
B.最小正周期为 的奇函数
的奇函数
C.最小正周期为 的偶函数
的偶函数
D.最小正周期为 的偶函数
的偶函数
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期期中数学试卷(解析版) 题型:填空题
关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c;②若a=(1,k),b=(-2,6),a∥b,则k=-3;③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为60°.其中真命题的序号为________.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com