
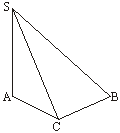
(Ⅰ)证明:SG∠BC;
(Ⅱ)求侧面SBC与底面ABC所成二面角的大小;
(Ⅲ)求三棱锥的体积VS-ABC.
(19)本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,考查逻辑思维能力、空间想象能力及运算能力.
解:
(Ⅰ)∵ ∠SAB=∠SAC=90°,
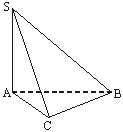 ∴ SA⊥AB,SA⊥AC.
∴ SA⊥AB,SA⊥AC.
又AB∩AC=A,
∴ SA⊥平面ABC.
又∠ACB=90°,即BC⊥AC,
根据三垂线定理,得SC⊥BC.
(Ⅱ)∵ BC⊥AC,SC⊥BC,
∴ ∠SCA是侧面SCB与底面ABC所成二面角的平面角.
在Rt△SCB中,
∵ BC=5,SB=5![]() ,
,
∴ SC=![]() =10.
=10.
在Rt△SAC中,
∵ SC=10,AC=5,
∴ cosSCA=![]() =
=![]() .
.
∴ ∠SCA=60°,即侧面SBC与底面ABC所成二面角的大小为60°.
(Ⅲ)在Rt△SAC中,
∵ SA=![]() ,
,
S△ABC =![]()
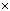 BC
BC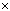 BC=
BC=![]() =
=![]() .
.
∴ VS—ABC=![]()
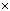 S△ACB
S△ACB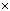 SA=
SA=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(Ⅰ)证明:SC⊥BC;
(Ⅱ)求侧面SBC与底面ABC所成二面角的大小;
(Ⅲ)求异面直线SC与AB所成的角的大小(用反三角函数表示).

查看答案和解析>>
科目:高中数学 来源: 题型:

(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角S—CM—A的大小;
(Ⅲ)求点B到平面SCM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N—CM—B的大小;
(Ⅲ)求点B到平面CMN的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com