已知集合A={x|-2<x<3},B={x|x2+2x-8>0},C={x|x2-4ax+3a2<0,a>0},若C⊆(A∩?RB),求实数a的取值范围.
解:由于B={x|x
2+2x-8>0}={x|x<-4,或x>2},
则?
RB={x|-4≤x≤2},
又由集合A={x|-2<x<3},故A∩?
RB={x|-2<x≤2},
而C={x|(x-a)(x-3a)<0}.
当a>0时,C={x|a<x<3a},
要使C⊆(A∩?
RB),则只需

,解得 0

故使C⊆(A∩?
RB)成立的实数a的取值范围为
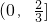
分析:利用因式分解法分别求出集合A,B,C,又由a>0,然后再根据交集、补集、子集的定义进行求解.
点评:此题主要考查子集的定义及其有意义的条件和集合的交集及补集运算,另外还考查了一元二次不等式的解法,
集合间的交、并、补运算是高考中的常考内容,要引起注意.

 ,解得 0
,解得 0
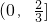


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案