
【题目】已知函数![]() .
.
(1)若函数![]() 存在极小值点,求
存在极小值点,求![]() 的取值范围;
的取值范围;
(2)证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先求导数,再讨论![]() 时与
时与![]() 时情况下导函数零点,根据导函数符号确定极值点取法,即得结果,(2)利用放缩法转化证
时情况下导函数零点,根据导函数符号确定极值点取法,即得结果,(2)利用放缩法转化证![]() ,(
,(![]() ),利用二次求导确定函数
),利用二次求导确定函数![]() 单调性,再根据单调性证不等式.
单调性,再根据单调性证不等式.
(1)由题意知,函数![]() 的定义域为
的定义域为![]()
![]()
①当![]() 时,令
时,令![]() ,解得
,解得![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 是函数
是函数![]() 的极小值点,满足题意.
的极小值点,满足题意.
②当![]() 时,令
时,令![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,无极值点,不满足题意.
上单调递增,无极值点,不满足题意.
若![]() ,即
,即![]() 时,
时,
![]() ,
,
∴![]() ,
,
又![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上恰有一个零点
上恰有一个零点![]() ,
,
当![]() 时
时![]() ,
,
当![]() 时
时![]() ,
,
∴![]() 是
是![]() 的极小值点,满足题意,
的极小值点,满足题意,
综上,![]() .
.
(2)当![]() 时
时![]()
若![]() 成立,
成立,
则![]() 必成立.
必成立.
①若![]() ,则
,则![]() ,
,![]()
∴![]() 成立
成立
∴![]() 成立.
成立.
②若![]() ,令
,令![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 时,
时,![]() 成立,
成立,
∴![]() 时,
时,![]() 成立,
成立,
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) |
晷影长(寸) | 135 |
|
|
|
|
节气 | 惊蛰(寒露) | 春分(秋分) | 清明(白露) | 谷雨(处暑) | 立夏(立秋) |
晷影长(寸) |
| 75.5 |
|
|
|
节气 | 小满(大暑) | 芒种(小暑) | 夏至 | ||
晷影长(寸) |
|
| 16.0 |
已知《易经》中记录的冬至晷影长为130.0寸,春分晷影长为72.4寸,那么《易经》中所记录的夏至的晷影长应为( )
A. 14.8寸B. 15.8寸C. 16.0寸D. 18.4寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为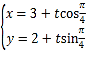 (其中
(其中![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
A. 众数 B. 平均数 C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求![]() 的概率
的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作.为做好全省的迎检工作,某市在高三年级开展了一次体质健康模拟测试(健康指数满分100分),并从中随机抽取了200名学生的数据,根据他们的健康指数绘制了如图所示的频率分布直方图.

(1)估计这200名学生健康指数的平均数![]() 和样本方差
和样本方差![]() (同一组数据用该组区间的中点值作代表);
(同一组数据用该组区间的中点值作代表);
(2)由频率分布直方图知,该市学生的健康指数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①求![]() ;
;
②已知该市高三学生约有10000名,记体质健康指数在区间![]() 的人数为
的人数为![]() ,试求
,试求![]() .
.
附:参考数据![]() ,
,
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为A,右焦点为F,且|AF|=3.
,左顶点为A,右焦点为F,且|AF|=3.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点F做互相垂直的两条直线l1,l2分别交直线l:x=4于M,N两点,直线AM,AN分别交椭圆于P,Q两点,求证:P,F,Q三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com