
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作.为做好全省的迎检工作,某市在高三年级开展了一次体质健康模拟测试(健康指数满分100分),并从中随机抽取了200名学生的数据,根据他们的健康指数绘制了如图所示的频率分布直方图.

(1)估计这200名学生健康指数的平均数![]() 和样本方差
和样本方差![]() (同一组数据用该组区间的中点值作代表);
(同一组数据用该组区间的中点值作代表);
(2)由频率分布直方图知,该市学生的健康指数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①求![]() ;
;
②已知该市高三学生约有10000名,记体质健康指数在区间![]() 的人数为
的人数为![]() ,试求
,试求![]() .
.
附:参考数据![]() ,
,
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某公司为了提高利润,从2014年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额x(万元) | 5 | 5.5 | 6 | 6.5 | 7 |
年利润增长y(万元) | 7.5 | 8 | 9 | 10 | 11.5 |
(1)请用最小二乘法求出y关于x的回归直线方程;
(2)如果2020年该公司计划对生产环节的改进的投资金额为8万元,估计该公司在该年的年利润增长为多少?
参考公式: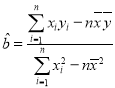 ,
,![]() 参考数据:
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.直线1的极坐标方程为
(α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.直线1的极坐标方程为![]() .
.
(Ⅰ)求C的普通方程和l的直角坐标方程;
(Ⅱ)设直线l与x轴和y轴的交点分别为A,B,点M在曲线C上,求△MAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
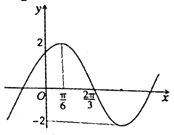
,![]() )的图象如图所示,令
)的图象如图所示,令![]() ,则下列关于函数
,则下列关于函数![]() 的说法中正确的是( )
的说法中正确的是( )
A. 函数![]() 图象的对称轴方程为
图象的对称轴方程为![]()
![]()
B. 函数![]() 的最大值为2
的最大值为2
C. 函数![]() 的图象上存在点
的图象上存在点![]() ,使得在
,使得在![]() 点处的切线与直线
点处的切线与直线![]() 平行
平行
D. 若函数![]() 的两个不同零点分别为
的两个不同零点分别为![]() ,
,![]() ,则
,则![]() 最小值为
最小值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com