Question

9．已知P是ABC所在平面内一点，$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\frac{3}{5}$$\overrightarrow{PA}$=$\overrightarrow{0}$，现将一粒黄豆随机撒在ABC内，则黄豆落在PBC内的概率是（　　）

• A． $\frac{3}{13}$
• B． $\frac{2}{3}$
• C． $\frac{3}{10}$
• D． $\frac{10}{13}$

Answer 1

分析 根据平面向量的运算性质得出P在AD上的位置，从而得出两三角形的面积比，得出几何概型的概率．

解答 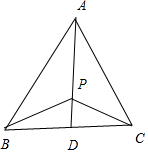解：取BC的中点D，连结PD，则$\overrightarrow{PB}+\overrightarrow{PC}$=2$\overrightarrow{PD}$，
∵$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\frac{3}{5}$$\overrightarrow{PA}$=$\overrightarrow{0}$，∴$\overrightarrow{PB}+\overrightarrow{PC}$=-$\frac{3}{5}$$\overrightarrow{PA}$，
∴2$\overrightarrow{PD}$=-$\frac{3}{5}$$\overrightarrow{PA}$，即$\overrightarrow{PD}$=-$\frac{3}{10}$$\overrightarrow{PA}$，
∴A，P，D三点共线，PD=$\frac{3}{13}$AD，
∴$\frac{{S}_{△PBC}}{{S}_{△ABC}}$=$\frac{3}{13}$，
∴黄豆落在PBC内的概率为$\frac{3}{13}$．
故选A．

点评 本题考查了平面向量的线性运算，几何概型的概率计算，属于中档题．