
分析 (1)由题意可得,代值计算即可,
(2)猜想,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(1)${b_1}=\frac{3}{4}$,${b_2}=\frac{4}{6}$,${b_3}=\frac{5}{8}$
(2)猜想:${b_n}=\frac{n+2}{2(n+1)}$
①n=1时,${b_1}=\frac{1+2}{4}=\frac{3}{4}$
②假设n=k时,${b_k}=\frac{k+2}{2(k+1)}$
当n=k+1时bk+1=(1-a1)(1-a2)…(1-ak)(1-ak+1)
=bk(1-ak+1)=$\frac{k+2}{2(k+1)}$(1-$\frac{1}{(k+2)^{2}}$)
=$\frac{k+2}{2(k+1)}$•$\frac{{k}^{2}+4k+3}{(k+2)^{2}}$=$\frac{(k+2)(k+1)(k+3)}{2(k+1)(k+2)^{2}}$=$\frac{k+3}{2(k+2)}$
综合①②:${b_n}=\frac{n+2}{2(n+1)}$.
点评 本题考查数列的递推公式,用数学归纳法证明等式成立.证明当n=k+1时命题也成立,是解题的难点.


科目:高中数学 来源: 题型:选择题
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
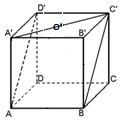 如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{13}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{10}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com