
已知集合 ,
, .
.
(1)当 时,求
时,求 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)先计算出 , 当
, 当 时,再计算出
时,再计算出 ,进而求两个集合的公共部分即可求出
,进而求两个集合的公共部分即可求出 ;(2)法一:先将
;(2)法一:先将 变形为
变形为 ,然后针对两根
,然后针对两根 、
、 的大小分
的大小分 、
、 、
、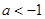 三类进行讨论,进而根据
三类进行讨论,进而根据 可求出
可求出 的取值范围;法二:根据
的取值范围;法二:根据 且
且 ,结合二次函数的图像与性质得到
,结合二次函数的图像与性质得到 ,从中求解即可得到
,从中求解即可得到 的取值范围.
的取值范围.
法一:(1) 2分
2分
当 时,
时, 4分
4分
∴ 6分
6分
(2) 7分
7分
①当 时,
时,
 不成立 9分
不成立 9分
②当 即
即 时,
时,
 ,
, ,解得
,解得 11分
11分
③当 即
即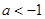 时,
时,
 解得
解得 13分
13分
综上,当 ,实数
,实数 的取值范围是
的取值范围是 14分(缺等号扣2分)
14分(缺等号扣2分)
法二:(1) 2分
2分
当 时,
时, 4分
4分
∴ 6分
6分
(2)记

 即
即 ,也就是
,也就是 10分
10分
解得 或
或
 实数
实数 的取值范围是
的取值范围是 14分 (缺等号扣2分).
14分 (缺等号扣2分).
考点:1.集合的运算;2.集合间的关系.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
(2012•广东)设a<1,集合A={x∈R|x>0},B={x∈R|2x2﹣3(1+a)x+6a>0},D=A∩B.
(1)求集合D(用区间表示);
(2)求函数f(x)=2x3﹣3(1+a)x2+6ax在D内的极值点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com