
【题目】以下资料是一位销售经理收集到的每年销售额y(千元)和销售经验x(年)的关系:
销售经验x/年 | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
年销售额y/千元 | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)依据这些数据画出散点图并作直线![]() =78+4.2x,计算
=78+4.2x,计算![]() ;
;
(2)依据这些数据求回归直线方程并据此计算![]() ;
;
(3)比较(1) (2)中的残差平方和![]() 的大小.
的大小.
【答案】(1)179.28; (2)![]() =80+4x; (3)(2)较小.
=80+4x; (3)(2)较小.
【解析】
对于(1),首先根据题目信息在坐标系中标出点,在连接即可得到散点图与直线y=78++4.2x,再根据x=1,3,…,13,得到![]() 的值代入计算即可得到答案;
的值代入计算即可得到答案;
对于(2)、(3),首先根据线性回归方程恒过样本中心点的性质,计算![]() 、
、![]() 的值,再根据
的值,再根据![]() 、
、![]() 的计算公式进行计算即可得到回归方程,再根据此方程令x=1,3,…,13,得到
的计算公式进行计算即可得到回归方程,再根据此方程令x=1,3,…,13,得到![]() 的值,代入计算即可得到
的值,代入计算即可得到![]() ,将其与(1)中的值比较即可得到答案.
,将其与(1)中的值比较即可得到答案.
(1)散点图与直线![]() =78+4.2x的图形如图,
=78+4.2x的图形如图,
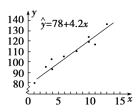 ,
,
对x=1,3,…,13,有
![]() i=82.2,90.6,94.8,94.8,103.2,111.6,120,120,124.2,132.6,
i=82.2,90.6,94.8,94.8,103.2,111.6,120,120,124.2,132.6,![]() =179.28.
=179.28.
(2)![]() =
=![]()
![]() ,
,![]()
∴![]() =
=![]() =4,
=4,![]() =
=![]() -
-![]()
![]() =108-7×4=80,
=108-7×4=80,
故![]() =80+4x.
=80+4x.
(3)对x=1,3,…,13,有
![]() =84,92,96,96,104,112,120,120,124,132,即
=84,92,96,96,104,112,120,120,124,132,即![]() 较小.
较小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1 , A2 , A3 , A4 , A5 , A6和4名女志愿者B1 , B2 , B3 , B4 , 从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(12分)
(Ⅰ)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(x+
=(sin(x+ ![]() ),1),
),1), ![]() =(4,4cosx﹣
=(4,4cosx﹣ ![]() )
)
(1)若 ![]() ⊥
⊥ ![]() ,求sin(x+
,求sin(x+ ![]() )的值;
)的值;
(2)设f(x)= ![]()
![]() ,若α∈[0,
,若α∈[0, ![]() ],f(α﹣
],f(α﹣ ![]() )=2
)=2 ![]() ,求cosα的值.
,求cosα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某书店共有韩寒的图书6种,其中价格为25元的有2种,18元的有3种,16元的有1种.书店若把这6种韩寒的图书打包出售,据统计每套的售价与每天的销售数量如下表所示:
售价x/元 | 105 | 108 | 110 | 112 |
销售数量y/套 | 40 | 30 | 25 | 15 |
(1)根据上表,利用最小二乘法得到回归直线方程![]() ,求
,求![]() ;
;
(2)若售价为100元,则每天销售的套数约为多少(结果保留到整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在复平面内对应的点在第一象限,且z=-3+4i.
(1)求z2及|z2|.
(2)若z1=z2,求θ与a2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对![]() 岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
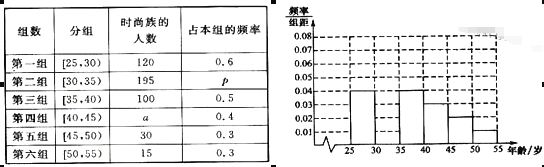
完成以下问题:
(Ⅰ)补全频率分布直方图并求![]() 的值;
的值;
(Ⅱ)从![]() 岁年龄段的“时尚族”中采用分层抽样法抽取
岁年龄段的“时尚族”中采用分层抽样法抽取![]() 人参加网络时尚达人大赛,其中选取
人参加网络时尚达人大赛,其中选取![]() 人作为领队,记选取的
人作为领队,记选取的![]() 名领队中年龄在
名领队中年龄在![]() 岁的人数为
岁的人数为![]() ,求
,求![]() 的分布列
的分布列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com