
已知数列{an}满足a1=2,an+1=an-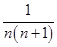 .
.
(1)求数列{an}的通项公式;
(2)设bn=nan·2n,求数列{bn}的前n项和Sn
(1) an=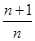 .(2) Sn=n·2n+1.
.(2) Sn=n·2n+1.
解析试题分析:(1)由已知得an+1-an=-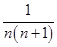 ,又a1=2,
,又a1=2,
∴当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=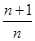 ,
,
a1=2也符合上式,∴对一切n∈N*,an=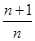 . 6分
. 6分
(2)由(1)知:bn=nan·2n=(n+1)·2n,
∴Sn=2×2+3×22+4×23+…+(n+1)×2n,①
2Sn=2×22+3×23+…+n×2n+(n+1)×2n+1,②
∴①-②得-Sn=2×2+22+23+…+2n-(n+1)×2n+1=2+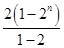 -(n+1)×2n+1
-(n+1)×2n+1
=2+2n+1-2-(n+1)·2n+1=-n·2n+1,∴Sn=n·2n+1. 12分
考点:本题考查了数列的通项公式及前n项和
点评:数列解答题考查的的热点为求数列的通项公式、等差(比)数列的性质及数列的求和问题.因此在复习中,要特别注意加强对由递推公式求通项公式、求有规律的非等差(比)数列的前n项和等的专项训练.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知数列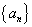 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
(1)求证:{ }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列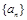 的前
的前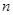 项和为
项和为 ,且满足
,且满足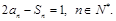
(1)求数列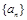 的通项公式;
的通项公式;
(2)在数列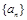 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列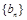 ,在
,在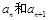 两项之间插入
两项之间插入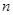 个数,使这
个数,使这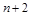 个数构成等差数列,求
个数构成等差数列,求 的值;
的值;
(3)对于(2)中的数列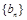 ,若
,若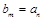 ,并求
,并求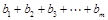 (用
(用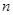 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;( 6分)
(2)设cn= ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com