Question

11．如图，在山顶C测得山下塔的塔顶A和塔底B的俯角分别为30°和60°，已知塔高AB为20m，则山高CD为30m．

Answer 1

分析 画图，塔底B测得高楼楼顶C的仰角为60°，所以∠DBC=60°=∠BCE，在高楼楼顶C测得塔顶A俯角为30°，所以∠ECA=30°，故∠ACB=∠ABC=30°∴AC=AB=40，作AF⊥CD，解直角三角形AFC求得FC，再加上FD即得CD的长．

解答 解：∵∠DBC=∠BCE=60°，∠ACE=30°，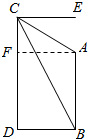
∴∠ACB=∠BCE-∠ACE=30°，∠ABC=90°-∠DBC=30°，
∴AC=AB=20m，
作AF⊥CD于点F，
∵∠CAF=∠ACE=30°，
∴CF=$\frac{1}{2}$AC=10m，
∴CD=CF+FD=CF+AB=20m+10m=30m．
故答案为：30m．

点评 本题考查三角形的应用，主要通过构造出可解的三角形，利用正弦，余弦定理及勾股定理求得相应边长或角度，考查了数形结合思想，属于中档题．