
| A. | 64π | B. | 68π | C. | 72π | D. | 100π |
分析 直角三角形ABC的外接圆的圆心为AB中点D,过D作面ABC的垂线,球心O在该垂线上,
过O作球的弦SC的垂线,垂足为E,则E为SC中点,球半径R=OS=$\sqrt{O{E}^{2}+S{E}^{2}}=\sqrt{C{D}^{2}+S{E}^{2}}$即可求出半径.
解答 解:如图所示,直角三角形ABC的外接圆的圆心为AB中点D,
过D作面ABC的垂线,球心O在该垂线上,
过O作球的弦SC的垂线,垂足为E,则E为SC中点,
球半径R=OS=$\sqrt{O{E}^{2}+S{E}^{2}}=\sqrt{C{D}^{2}+S{E}^{2}}$
∵$CD=\frac{1}{2}AB=4$,SE=3,∴R=5
棱锥的外接球的表面积为4πR2=100π,
故选:D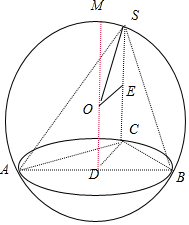
点评 本题考查了球的内接三棱锥,解题的关键是找到数量关系,求出球半径,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:解答题
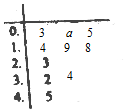 已知函数f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,现有一组数据(该组数据数量庞大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.
已知函数f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,现有一组数据(该组数据数量庞大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
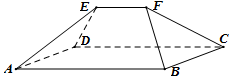 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )| A. | $8\sqrt{3}$ | B. | $8+8\sqrt{3}$ | C. | $6\sqrt{2}+2\sqrt{3}$ | D. | $8+6\sqrt{2}+2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5人 | B. | 6人 | C. | 7人 | D. | 8人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com