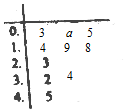Question

6．已知函数f（x）=x²+$\sqrt{2}$（m-1）x+$\frac{m}{4}$，现有一组数据（该组数据数量庞大），从中随机抽取10个，绘制所得的茎叶图如图所示，且茎叶图中的数据的平均数为2．
（1）现从茎叶图中的数据中任取4个数据分别替换m的值，求至少有2个数据使得函数f（x）没有零点的概率；
（2）以频率估计概率，若从该组数据中随机抽取4个数据分别替换m的值，记使得函数f（x）没有零点的个数为?，求?的分布列以及数学期望、方差．

Answer 1

分析 （1）根据平均数求出a，根据二次函数的性质求出f（x）无零点的条件，利用超几何分布的概率计算公式计算；
（2）按照超几何分布依次计算概率，得出分布列，代入公式计算数学期望和方差．

解答 解：（1）∵茎叶图中的数据的平均数为2，
∴0.3+$\frac{a}{10}$+0.5+1.4+1.9+1.8+2.3+3.2+3.4+4.5=2×10，解得a=7，
若要是f（x）无零点，则△=2（m-1）²-m＜0，解得0.5＜m＜2．
而茎叶图中的10个数据中只有4个符合条件，
故而至少有2个数据使得函数f（x）没有零点的概率P=$\frac{{C}_{4}^{2}{•C}_{6}^{2}{+C}_{4}^{3}•{C}_{6}^{1}{+C}_{4}^{4}}{{C}_{10}^{4}}$=$\frac{25}{42}$．
（2）?的可能取值为0，1，2，3，4，显然?服从超几何分布，其中N=10，M=4，n=4，
则P（?=0）=$\frac{{C}_{6}^{4}}{{C}_{10}^{4}}$=$\frac{1}{14}$，P（?=1）=$\frac{{C}_{4}^{1}{•C}_{6}^{3}}{{C}_{10}^{4}}$=$\frac{8}{21}$，P（?=2）=$\frac{{C}_{4}^{2}{•C}_{6}^{2}}{{C}_{10}^{4}}$=$\frac{3}{7}$，P（?=3）=$\frac{{C}_{4}^{3}{•C}_{6}^{1}}{{C}_{10}^{4}}$=$\frac{4}{35}$，P（?=4）=$\frac{{C}_{4}^{4}}{{C}_{10}^{4}}$=$\frac{1}{210}$．
∴?的分布列为：

?	0	1	2	3	4
P	$\frac{1}{14}$	$\frac{8}{21}$	$\frac{3}{7}$	$\frac{4}{35}$	$\frac{1}{210}$

∴E（?）=$\frac{4}{10}×4$=$\frac{8}{5}$．
D（?）=$\frac{4×4×（10-4）（10-4）}{1{0}^{2}×（10-1）}$=$\frac{16}{25}$．

点评 本题考查了茎叶图，离散型随机变量的数学期望和方差，超几何分布，属于中档题．