
| A. | ($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2) | B. | ($\frac{1}{2}$,2) | C. | (-$\frac{1}{2}$,-2) | D. | ($\frac{1}{2}$,-2) |
分析 求出y′=-$\frac{1}{{x}^{2}}$,设P(x0,$\frac{1}{{x}_{0}}$),由在点P处的切线斜率为-4,利用导数的几何意义得到-$\frac{1}{{{x}_{0}}^{2}}$=-4,由此能求出点P的坐标.
解答 解:∵曲线y=$\frac{1}{x}$,∴y′=-$\frac{1}{{x}^{2}}$,
设P(x0,$\frac{1}{{x}_{0}}$),
∵在点P处的切线斜率为-4,∴-$\frac{1}{{{x}_{0}}^{2}}$=-4,解得${x}_{0}=\frac{1}{2}$或${x}_{0}=-\frac{1}{2}$,
∴点P的坐标是($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2).
故选:A.
点评 本题考查点的坐标的求法,涉及到导数、切线、导数的几何意义关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
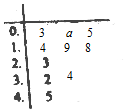 已知函数f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,现有一组数据(该组数据数量庞大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.
已知函数f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,现有一组数据(该组数据数量庞大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5人 | B. | 6人 | C. | 7人 | D. | 8人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com