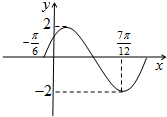Question

1．已知函数f（x）=Asin（ωx+φ）（A，ω＞0，-π＜φ＜π）在一个周期内的图象如图所示．
（1）求f（x）的表达式；
（2）在△ABC中，f（C+$\frac{π}{6}$）=-1且$\overrightarrow{CA}$•$\overrightarrow{CB}$＜0，求角C．

Answer 1

分析 （1）由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，从而求得函数f（x）的表达式．
（2）利用（1）及f（C$+\frac{π}{6}$）=-1可得sin（2C$+\frac{2π}{3}$）=-$\frac{1}{2}$，结合角的范围可求C=$\frac{π}{4}$或$\frac{7π}{12}$，利用平面向量数量积的运算可求cosC＜0，从而可求C的值．

解答 解：（1）由图可知函数的最大值是2，最小值是-2，
∴A=2，…（1分）
∵$\frac{3}{4}$T=$\frac{7π}{12}$+$\frac{π}{6}$=$\frac{3π}{4}$，
∴T=π=$\frac{2π}{ω}$，可得：ω=2，…（2分）
又∵f（x）过点（-$\frac{π}{6}$，0），且根据图象特征得：-2×$\frac{π}{6}$+φ=0+2kπ，k∈Z，
∴φ=$\frac{π}{3}$+2kπ，k∈Z，…（4分）
而-π＜φ＜π，
∴φ=$\frac{π}{3}$．…（5分）
∴f（x）=2sin（2x+$\frac{π}{3}$）．…（6分）
（2）∵f（x）=2sin（2x+$\frac{π}{3}$），
∴f（C$+\frac{π}{6}$）=2sin（2C$+\frac{2π}{3}$）=-1，…（7分）
∴sin（2C$+\frac{2π}{3}$）=-$\frac{1}{2}$，…（9分）
因为C为三角形内角，
∴C=$\frac{π}{4}$或$\frac{7π}{12}$，…（10分）
又∵$\overrightarrow{CA}$•$\overrightarrow{CB}$=abcosC＜0，0＜C＜π，
∴cosC＜0，$\frac{π}{2}$＜C＜π，
∴C=$\frac{7π}{12}$．．…（12分）

点评 本题主要考查由函数y=Asin（ωx+∅）的部分图象求解析式，考查了平面向量数量积的运算，正弦函数的图象和性质的应用，考查了数形结合思想，属于中档题．