
分析 (1)一般认为,人的年龄与他(她)拥有的财富有相关关系;
(2)曲线上的点与该点的坐标之间是一种函数关系;
(3)苹果的产量受当地气候的影响,是相关关系;
(4)森林中的同一种树木,其断面直径与高度之间的关系是一种相关关系;
(5)学生与他(她)的学号之间映射.
解答 解:对于(1),人的年龄与他(她)拥有的财富是相关关系,∴(1)满足条件;
对于(2),曲线上的点与该点的坐标之间是一种函数关系,不是相关关系,∴(2)不满足条件;
对于(3),苹果的产量与气候之间是一种相关关系,∴(3)满足条件;
对于(4),森林中的同一种树木,其断面直径与高度之间的关系是一种相关关系,∴(4)满足条件;
对于(5),学生与他(她)的学号之间的关系,是一种映射,不是相关关系,∴(5)不满足条件;
综上,其中有相关关系的是(1)(3)(4).
故答案为:(1)(3)(4).
点评 判断两个变量间的关系是函数关系还是相关关系的关键是判断两个变量之间的关系是否是确定的,若确定的则是函数关系;若不确定,则是相关关系.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1 } | B. | {-1,0} | C. | {-1,1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
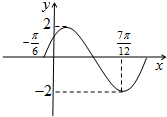 已知函数f(x)=Asin(ωx+φ)(A,ω>0,-π<φ<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A,ω>0,-π<φ<π)在一个周期内的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| ≥170cm | <170cm | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com