解:(1)f′(x)=3x
2+2ax+6
由已知得


解得
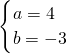
∴f(x)=x
3+4x
2-3x
(2)由已知只须f(x)max≤m+

f′(x)=3x
2+8x-3
令f′(x)>0解得x>

或x<-3
则f(x)在(

,+∞)和(-∞,3)上单调递增
令f′(x)<0,解得-3<x<

则f(x)在(-3,

)上单调递减
∴f(x)在[-1,

]上单调递减
在[

,1]上单调递增:
f(-1)=-1+4+3=6
f(1)=1+4-3=2
∴f(x)max=6.
则m+

≥6,由m>0,得m
2-6m+5≥0,解得m≥5或0<m≤1
分析:(1)根据f(x)在点P(1,2)处的切线与直线y=8x+1平行建立两个等式关系,f'(1)=8,f(1)=2,解方程组即可求出a与b的值;
(2)将
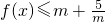
在[-1,1]上恒成立转化成f(x)max≤m+

,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,然后解不等式f(x)max≤m+

,即可求出m的取值范围.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等基础题知识,考查运算求解能力、推理论证能力,考查化归与转化思想,属于基础题.

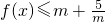 在[-1,1]上恒成立,求正数m的取值范围.
在[-1,1]上恒成立,求正数m的取值范围.

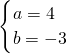

 或x<-3
或x<-3 ,+∞)和(-∞,3)上单调递增
,+∞)和(-∞,3)上单调递增
 )上单调递减
)上单调递减 ]上单调递减
]上单调递减 ,1]上单调递增:
,1]上单调递增: ≥6,由m>0,得m2-6m+5≥0,解得m≥5或0<m≤1
≥6,由m>0,得m2-6m+5≥0,解得m≥5或0<m≤1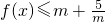 在[-1,1]上恒成立转化成f(x)max≤m+
在[-1,1]上恒成立转化成f(x)max≤m+ ,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,然后解不等式f(x)max≤m+
,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,然后解不等式f(x)max≤m+ ,即可求出m的取值范围.
,即可求出m的取值范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<