
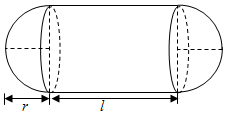
 某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.
某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.分析 (1)求出半球与圆柱的面积,得出y关于r的函数;
(2)令y≤80,解出r的最大值,从而得出体积V的最大值.
解答 解:(1)半球的表面积${S_1}=2π{r^2}$,圆柱的表面积S2=2πr•l.
于是$y=3×2{S_1}+1×{S_2}=3×4π{r^2}+1×2πr•(2r+1)=16π{r^2}+2πr$.
定义域为$[{\frac{1}{2},+∞})$.
(2)16πr2+2πr≤80,即${r^2}+\frac{1}{8}r-\frac{5}{π}≤0$,解得$r≤\frac{{-\frac{1}{8}+\sqrt{\frac{1}{64}+\frac{20}{π}}}}{2}≈1.2$.
$V=\frac{4}{3}π{r^3}+π{r^2}•(2r+1)=\frac{10}{3}π{r^3}+π{r^2}$,
经计算得V≈22.7(立方米).
故r的最大值为1.2(米),此时储油罐的体积约为22.7立方米.
点评 本题考查了空间几何体的面积与体积计算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
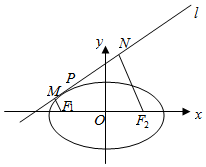 如图,在平面直角坐标系xOy中,直线l与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相切于点P,过椭圆的左、右焦点F1,F2分别作F1M,F2N重直于直线l于M,N,记μ=$\frac{{N{F_2}}}{{M{F_1}}}$,当P为左顶点时,μ=9,且当μ=1时,四边形MF1F2N的周长为22.
如图,在平面直角坐标系xOy中,直线l与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相切于点P,过椭圆的左、右焦点F1,F2分别作F1M,F2N重直于直线l于M,N,记μ=$\frac{{N{F_2}}}{{M{F_1}}}$,当P为左顶点时,μ=9,且当μ=1时,四边形MF1F2N的周长为22.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com