
分析 (1)由题意求得A,B的坐标,由椭圆离心率、三角形F1AB的面积及隐含条件列方程组,求解方程组得a2,b2的值,则椭圆方程可求;
(2)设P(x1,y1),Q(x2,y2),联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求得x1x2,y1y2的值,结合OP⊥OQ,即x1x2+y1y2=0,求得m与k的关系,并得到m的范围,由圆心到直线的距离求得圆的半径,得到存在圆x2+y2=$\frac{8}{3}$使得l恰好是该圆的切线.
解答 解:(1)设F1(-c,0),F2(c,0),
∵AB⊥F1F2,∴设A(c,y0),B(c,-y0),其中y0>0,
又∵A,B在椭圆上,∴$\frac{{c}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$,解得${y}_{0}=\frac{{b}^{2}}{a}$.
∵$e=\frac{c}{a}=\frac{\sqrt{2}}{2}$,△F1AB的面积为4$\sqrt{2}$.
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{2}•2c•\frac{2{b}^{2}}{a}=4\sqrt{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=8,b2=4.
∴椭圆C的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)设P(x1,y1),Q(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(1+2k2)x2+4kmx+2m2-8=0.
∵△=16k2m2-4(1+2k2)(2m2-8)=64k2-8m2+32>0
∴8k2-m2+4>0.①
${x}_{1}+{x}_{2}=-\frac{4km}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{2{m}^{2}-8}{1+2{k}^{2}}$.
${y}_{1}{y}_{2}=(k{x}_{1}+m)(k{x}_{2}+m)={k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}$=$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$.
∵OP⊥OQ,∴x1x2+y1y2=0,即$\frac{2{m}^{2}-8}{1+2{k}^{2}}+\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}=0$.
∴${k}^{2}=\frac{3{m}^{2}-8}{8}$>0.②
联立①②得,${m}^{2}≥\frac{8}{3}$.
∵l与圆x2+y2=r2相切,∴${r}^{2}=\frac{|m{|}^{2}}{1+{k}^{2}}=\frac{8}{3}$.
∴存在圆x2+y2=$\frac{8}{3}$使得l恰好是该圆的切线.
点评 本题考查椭圆标准方程的求法,考查了直线与圆锥曲线位置关系的应用,体现了“设而不求”及“整体运算”思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
 椭圆M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,点P(0,2)关于直线y=-x的对称点在椭圆M上.
椭圆M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,点P(0,2)关于直线y=-x的对称点在椭圆M上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
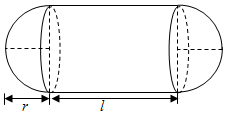 某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.
某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)关于x=$\frac{5}{9}$π对称 | |
| B. | 函数f(x)向左平移$\frac{π}{18}$个单位后是奇函数 | |
| C. | 函数f(x)关于点($\frac{π}{18}$,0)中心对称 | |
| D. | 函数f(x)在区间[0,$\frac{π}{20}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com