
分析 根据C=π-B-A将cosC化为角B、A的关系即可证
解答 (2)∵cosC=cos[π-(A+B)]=-cos(A+B)=sinAsinB-cosAcosB.
∴cos2A+cos2B+cos2C+2cosAcosBcosC
=cos2A+cos2B+cos2Acos2B+sin2Asin2B-2cosAcosBsinAsinB+2cosAcosBcosC
=cos2A+cos2B+cos2Acos2B+(1-cos2A)(1-cos2B)-2cosAcosBsinAsinB+2cosAcosBcosC
=1-2[cos2Acos2B-cosAcosBsinAsinB]+2cosAcosBcosC
=1-2cosAcosB(cosAcosB-sinAsinB)+2cosAcosBcosC
=1-2cosAcosBcos(A+B)+2cosAcosBcosC
=1-2cosAcosBcos[π-(A+B)]+2cosAcosBcosC
=1-2cosAcosBcosC+2cosAcosBcosC
=1.
点评 本题主要考查三角函数的基本关系式.这里要注意的试在三角形中三个角的和为π,经常通过一个角等于π减另外两个角来转化


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
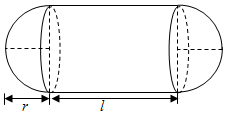 某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.
某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
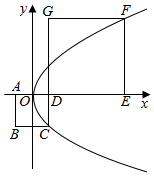 如图,正方形ABCD中,坐标原点O为AD的中点,正方形DEFG的边长为b,若D为抛物线y2=2ax(0<a<b)的焦点,且此抛物线经过C,F两点,则$\frac{b}{a}$=1+$\sqrt{2}$.
如图,正方形ABCD中,坐标原点O为AD的中点,正方形DEFG的边长为b,若D为抛物线y2=2ax(0<a<b)的焦点,且此抛物线经过C,F两点,则$\frac{b}{a}$=1+$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com