
分析 题目给出的是含有绝对值的定积分,计算时根据被积函数的零点分段,所以需要把积分区间分成两段,然后把被积函数去绝对值后再求积分.
解答 解:|x-2|=$\left\{\begin{array}{l}{x-2}&{x≥2}\\{2-x}&{x<2}\end{array}\right.$,
∴${∫}_{0}^{3}$|x-2|dx=${∫}_{0}^{2}(2-x)dx$+${∫}_{2}^{3}(x-2)dx$=(2x-$\frac{1}{2}$x2)${丨}_{0}^{2}$+($\frac{1}{2}$x2-2x)${丨}_{2}^{3}$,
=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题考查了定积分,解答此题时首先要熟练掌握微积分基本定理,同时注意含有绝对值的定积分要分段求解,属于基础题.


科目:高中数学 来源: 题型:解答题
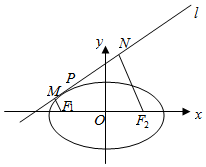 如图,在平面直角坐标系xOy中,直线l与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相切于点P,过椭圆的左、右焦点F1,F2分别作F1M,F2N重直于直线l于M,N,记μ=$\frac{{N{F_2}}}{{M{F_1}}}$,当P为左顶点时,μ=9,且当μ=1时,四边形MF1F2N的周长为22.
如图,在平面直角坐标系xOy中,直线l与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相切于点P,过椭圆的左、右焦点F1,F2分别作F1M,F2N重直于直线l于M,N,记μ=$\frac{{N{F_2}}}{{M{F_1}}}$,当P为左顶点时,μ=9,且当μ=1时,四边形MF1F2N的周长为22.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$](k∈Z) | ||
| C. | [$\frac{2kπ}{3}$-$\frac{π}{18}$,$\frac{2kπ}{3}$+$\frac{5π}{18}$](k∈Z) | D. | [$\frac{2kπ}{3}$-$\frac{7π}{18}$,$\frac{2kπ}{3}$-$\frac{π}{18}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
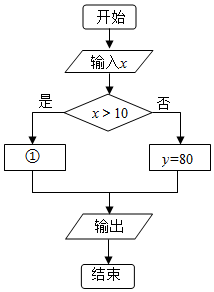 某海滨游乐场出租快艇的收费办法如下:不超过十分钟收费80元;超过十分钟,超过部分按每分钟10元收费(对于其中不足一分钟的部分,若小于0.5分钟则不收费,若大于或等于0.5分钟则按一分钟收费),小茗同学为该游乐场设计了一款收费软件,程序框图如图所示,其中x(分钟)为航行时间,y(元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
某海滨游乐场出租快艇的收费办法如下:不超过十分钟收费80元;超过十分钟,超过部分按每分钟10元收费(对于其中不足一分钟的部分,若小于0.5分钟则不收费,若大于或等于0.5分钟则按一分钟收费),小茗同学为该游乐场设计了一款收费软件,程序框图如图所示,其中x(分钟)为航行时间,y(元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )| A. | y=10[x] | B. | y=10[x]-20 | C. | y=10[x-$\frac{1}{2}$]-20 | D. | y=10[x+$\frac{1}{2}$]-20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com