
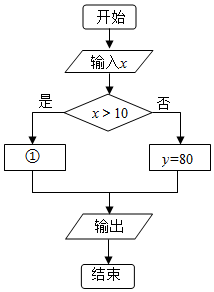
 某海滨游乐场出租快艇的收费办法如下:不超过十分钟收费80元;超过十分钟,超过部分按每分钟10元收费(对于其中不足一分钟的部分,若小于0.5分钟则不收费,若大于或等于0.5分钟则按一分钟收费),小茗同学为该游乐场设计了一款收费软件,程序框图如图所示,其中x(分钟)为航行时间,y(元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
某海滨游乐场出租快艇的收费办法如下:不超过十分钟收费80元;超过十分钟,超过部分按每分钟10元收费(对于其中不足一分钟的部分,若小于0.5分钟则不收费,若大于或等于0.5分钟则按一分钟收费),小茗同学为该游乐场设计了一款收费软件,程序框图如图所示,其中x(分钟)为航行时间,y(元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )| A. | y=10[x] | B. | y=10[x]-20 | C. | y=10[x-$\frac{1}{2}$]-20 | D. | y=10[x+$\frac{1}{2}$]-20 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
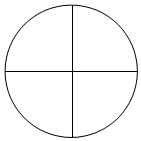 用4种不同的颜色涂下列区域,要求每个区域只能用一种颜色,且相邻的区域不能同色,那么不同的涂法种数为( )
用4种不同的颜色涂下列区域,要求每个区域只能用一种颜色,且相邻的区域不能同色,那么不同的涂法种数为( )| A. | 84 | B. | 72 | C. | 60 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com