练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．曲线y=x3的拐点坐标为（0，0）．

    分析 根据曲线的拐点的定义，要先进行二阶求导，然后求导数为0的点及导数的正负．

    解答 解：∵y′=3x2，
    ∴y″=6x，
    令y″=0，
    解得，x=0，
    ∴曲线y=x3的拐点坐标为（0，0）
    故答案为：（0，0）．

    点评 本题考查内容集中在曲线的特征上，拐点的概念要理解并掌握．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，过右焦点F且垂直于x轴的直线与椭圆C相交于M，N两点，且|MN|=3．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设直线l经过点F且斜率为k，l与椭圆C相交于A，B两点，与以椭圆C的右顶点E为圆心的圆相交于P，Q两点（A，P，B，Q自下至上排列），O为坐标原点．若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{9}{5}$，且|AP|=|BQ|，求直线l和圆E的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．直线y=kx-k+1与椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1的位置关系是（　　）
    A．相交B．相切C．相离D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

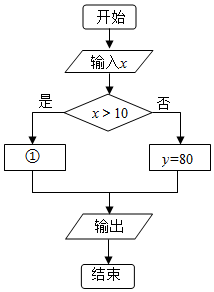    9．某海滨游乐场出租快艇的收费办法如下：不超过十分钟收费80元；超过十分钟，超过部分按每分钟10元收费（对于其中不足一分钟的部分，若小于0.5分钟则不收费，若大于或等于0.5分钟则按一分钟收费），小茗同学为该游乐场设计了一款收费软件，程序框图如图所示，其中x（分钟）为航行时间，y（元）为所收费用，用[x]表示不大于x的最大整数，则图中①处应填（　　）
    A．y=10[x]B．y=10[x]-20C．y=10[x-$\frac{1}{2}$]-20D．y=10[x+$\frac{1}{2}$]-20

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知PQ是圆x2+y2=100的动弦，|PQ|=12，则PQ中点的轨迹方程是（　　）
    A．x2+y2=8B．x2+y2=64C．x2+y2=36D．x2+y2=6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若a＜-8，则|6-$\sqrt{（a+1）^{2}}$|等于（　　）
    A．5-aB．-a-7C．a+7D．a-5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知tanα=$\frac{1}{2}$，则sin2α-sin2α的值是$-\frac{3}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设f（x）=$\frac{a}{x}$+xlnx，g（x）=x3-x2-3．
    （1）当a=1时，求f（x）在点（1，1）处的切线方程．
    （2）如果对任意的$s，t∈[\frac{1}{2}，2]$，都有f（s）≥g（t）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．直线y=a（a为常数）与y=tanωx（ω＞0）的相邻两支的交点距离为（　　）
    A．πB．$\frac{π}{ω}$C．$\frac{π}{2ω}$D．与a有关的值

    查看答案和解析>>

    同步练习册答案