练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
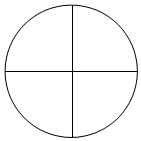
    19．用4种不同的颜色涂下列区域，要求每个区域只能用一种颜色，且相邻的区域不能同色，那么不同的涂法种数为（　　）
    A．84B．72C．60D．120

    分析 ①若AD区域涂不同的颜色，②若AD号区域涂相同的颜色，两种情况讨论其他区域的涂色方案，由分类计数原理可得．

    解答 解：①若AD区域涂不同的颜色，A有4种，D有3种，B有2种，C有2种，共有4×3×2×2=48种，
    ②若AD区域涂相同的颜色，A有4种，B有3种，C有3种，共有4×3×3=36种，
    故有48+36=84，
    故选：A．

    点评 本题考查分步计数原理与分类计数原理的综合运用，注意4个区域的位置关系即可

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．P为抛物线y2=4x上任意一点，P在y轴上的射影为Q，点M（7，8），则|PM|与|PQ|长度之和的最小值为9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．如图，点F1，F2分别是椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，点A是下顶点，抛物线C2：y=x2-1与x轴交于点F1，F2，与y轴交于点B，且点B是线段OA的中点，点N为抛物线上C2的一动点，过点N作抛物线C2的切线交椭圆C1于P，Q两点．
    （1）求椭圆C1的方程；
    （2）若点M（0，-$\frac{4}{5}$），求△MPQ面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．为考查某种疫苗预防疾病的效果，进行动物实验，得到统计数据如表：
    未发病发病合计
    未注射疫苗20xA
    注射疫苗30yB
    合计5050100
    现从所有试验动物中任取一只，取到“注射疫苗”动物的概率为$\frac{2}{5}$．
    （1）求2×2列联表中的数据x，y，A，B的值；
    （2）绘制发病率的条形统计图，并判 断疫苗是否有效？
    （3）能够有多大把握认为疫苗有效？
    附：K2=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
    P（ K2≤K0）0.050.010.0050.001
    K03.8416.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求满足以C（2，-1）为圆心且与直线3x-4y-5=0相切圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

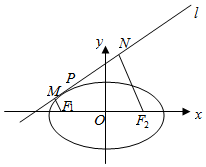    4．如图，在平面直角坐标系xOy中，直线l与椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）相切于点P，过椭圆的左、右焦点F1，F2分别作F1M，F2N重直于直线l于M，N，记μ=$\frac{{N{F_2}}}{{M{F_1}}}$，当P为左顶点时，μ=9，且当μ=1时，四边形MF1F2N的周长为22．
    （1）求椭圆的标准方程；
    （2）求证：MF1•NF2为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，过右焦点F且垂直于x轴的直线与椭圆C相交于M，N两点，且|MN|=3．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设直线l经过点F且斜率为k，l与椭圆C相交于A，B两点，与以椭圆C的右顶点E为圆心的圆相交于P，Q两点（A，P，B，Q自下至上排列），O为坐标原点．若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{9}{5}$，且|AP|=|BQ|，求直线l和圆E的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知方程$\frac{{x}^{2}}{5-2m}$+$\frac{{y}^{2}}{m+1}$=1表示椭圆，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

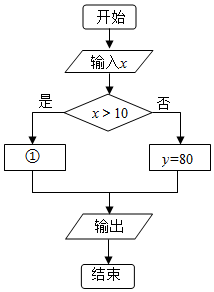    9．某海滨游乐场出租快艇的收费办法如下：不超过十分钟收费80元；超过十分钟，超过部分按每分钟10元收费（对于其中不足一分钟的部分，若小于0.5分钟则不收费，若大于或等于0.5分钟则按一分钟收费），小茗同学为该游乐场设计了一款收费软件，程序框图如图所示，其中x（分钟）为航行时间，y（元）为所收费用，用[x]表示不大于x的最大整数，则图中①处应填（　　）
    A．y=10[x]B．y=10[x]-20C．y=10[x-$\frac{1}{2}$]-20D．y=10[x+$\frac{1}{2}$]-20

    查看答案和解析>>

    同步练习册答案