
 Ϊ����ij������Ԥ��������Ч�������ж���ʵ�飬�õ�ͳ�����������
Ϊ����ij������Ԥ��������Ч�������ж���ʵ�飬�õ�ͳ�����������| δ���� | ���� | �ϼ� | |
| δע������ | 20 | x | A |
| ע������ | 30 | y | B |
| �ϼ� | 50 | 50 | 100 |
| P�� K2��K0�� | 0.05 | 0.01 | 0.005 | 0.001 |
| K0 | 3.841 | 6.635 | 7.879 | 10.828 |
���� ��1���ɡ�ע�����硱����ĸ���Ϊ$\frac{2}{5}$���ɵ�$\frac{y+30}{100}=\frac{2}{5}$�����yֵ����һ�����x��A��ֵ��
��2����ͼ��ֱ�����δע�����緢����Ϊ$\frac{40}{60}=\frac{2}{3}$��ע�����緢����Ϊ$\frac{10}{40}=\frac{1}{4}$�������������ʵ�����ͳ��ͼ����ͼ�õ�������Ч��
��3����2��2���������K2��ֵ����Ӧ�����ô𰸣�
��� �⣺��1���衰���������鶯������ȡһֻ��ȡ����ע�����硱���Ϊ�¼� M��
����֪��P��M��=$\frac{y+30}{100}=\frac{2}{5}$��
��y=10��B=40��x=40��A=60������5�֣�
��2��δע�����緢����Ϊ$\frac{40}{60}=\frac{2}{3}$��ע�����緢����Ϊ$\frac{10}{40}=\frac{1}{4}$��
�����ʵ�����ͳ��ͼ��ͼ��ʾ������7�֣�
��ͼ���Կ���������Ч������8�֣�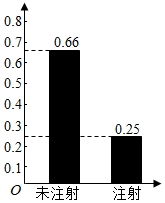
��3��${{K}^2}=\frac{{100{{��{20��10-30��40}��}^2}}}{50��50��40��60}$����9�֣�
=$\frac{1000000}{50��20��60}=\frac{50}{3}��16.67��10.828$������11�֣�
����99.9%�İ�����Ϊ������Ч������12�֣�
���� ���⿼������Լ����Ӧ�ã�������ѧ����ȡͼ��������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
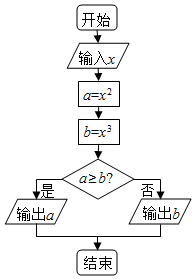
| A�� | 16 | B�� | 4 | C�� | 64 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
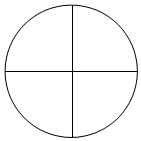 ��4�ֲ�ͬ����ɫͿ��������Ҫ��ÿ������ֻ����һ����ɫ�������ڵ�������ͬɫ����ô��ͬ��Ϳ������Ϊ��������
��4�ֲ�ͬ����ɫͿ��������Ҫ��ÿ������ֻ����һ����ɫ�������ڵ�������ͬɫ����ô��ͬ��Ϳ������Ϊ��������| A�� | 84 | B�� | 72 | C�� | 60 | D�� | 120 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com