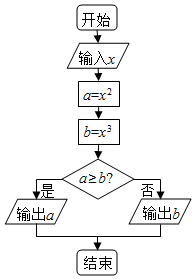
执行如图所示的程序框图.若输入的x的值为4.则输出的数是( )A．16B．4C．64D．8 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

12．执行如图所示的程序框图，若输入的x的值为4，则输出的数是（　　）

A．

B．

C．

D．

分析根据题意，模拟程序框图的运行过程，即可得出输出的结果．

解答解：模拟执行程序，可得
x=4，a=16，b=64
不满足条件a≥b，输出b的值为64．
故选：C．

点评本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，即可得出正确的答案，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

2．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程是$ρcos（θ-\frac{π}{4}）=2\sqrt{2}$，圆C的极坐标方程是ρ=4sinθ．
（Ⅰ）求l与C交点的极坐标；
（Ⅱ）设P为C的圆心，Q为l与C交点连线的中点，已知直线PQ的参数方程是$\left\{\begin{array}{l}x=\root{3}{t}+a\\ y=\frac{b}{2}\root{3}{t}+1\end{array}\right.$（t为参数），求a，b的值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+4x，0≤x＜4}\\{lo{g}_{2}（x+4），4≤x≤12}\end{array}\right.$，若存在x₁，x₂∈R，当0≤x₁＜4≤x₂≤12时，f（x₁）=f（x₂），则x₁f（x₂）的最大值是$\frac{256}{27}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．已知x，y，z都是正数且xyz=8，求证：（2+x）（2+y）（2+z）≥64．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．

为考查某种疫苗预防疾病的效果，进行动物实验，得到统计数据如表：

	未发病	发病	合计
未注射疫苗	20	x	A
注射疫苗	30	y	B
合计	50	50	100

现从所有试验动物中任取一只，取到“注射疫苗”动物的概率为$\frac{2}{5}$．
（1）求2×2列联表中的数据x，y，A，B的值；
（2）绘制发病率的条形统计图，并判断疫苗是否有效？
（3）能够有多大把握认为疫苗有效？
附：K²=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$

P（ K²≤K₀）	0.05	0.01	0.005	0.001
K₀	3.841	6.635	7.879	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

17．高二某个班第二组有13位同学，其中女生6人，男生7人，并且男，女生各有一名队长，现从中挑出5名同学参加学校组织的大扫除，依下列条件各有多少种选法？
（1）只有一名女生被选到；
（2）至少一名队长被选到；
（3）既要有队长，又要有男生被选到．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

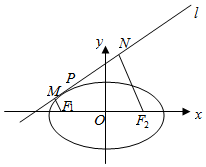如图，在平面直角坐标系xOy中，直线l与椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）相切于点P，过椭圆的左、右焦点F₁，F₂分别作F₁M，F₂N重直于直线l于M，N，记μ=$\frac{{N{F_2}}}{{M{F_1}}}$，当P为左顶点时，μ=9，且当μ=1时，四边形MF₁F₂N的周长为22．
（1）求椭圆的标准方程；
（2）求证：MF₁•NF₂为定值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．已知不等式x²+bx-b-$\frac{3}{4}$＞0的解集为R，则b的取值范围是（-3，-1）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．3个男生和2个女生站成一排拍照，两个女生必须站在一起，且不能站在两端，不同的站法数是（　　）

A．

B．

C．

D．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学