
���� ��1������Բ������A�����bֵ���������ʼ�a2=b2+c2�����aֵ���Ӷ�����Բ���̣�
��2����ֱ�߷���y=kx+t��A��B������꣬��ֱ�߷��̴�����Բ���̣�������������x��һԪ���η��̣�����Τ�ﶨ���ֱ����x1+x2��x1•x3��ֵ��д��y1+y2��y1•y2�ı���ʽ��������ABΪֱ����Բ��ԭ�㣬��֪$\overrightarrow{OA}•\overrightarrow{OB}=0$���������������������껯������5t2=4+4k2������0�����t��-$\frac{\sqrt{3}}{2}$��t��$\frac{\sqrt{3}}{2}$������е����꣬���е����깫ʽ��ֱ��PD��ֱ��l��ֱ�����t��ֵ���������k��ֵ��д��ֱ�߷��̣�
��� �⣺��1���������$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\end{array}\right.$��a2=b2+c2����ã�a=2��b=1��
������ԲC�ķ�����$\frac{{x}^{2}}{4}+{y}^{2}=1$�� ����4�֣�
��2����ֱ��l�ķ���Ϊy=kx+t����A��x1��y1����B��x2��y2����
����$\left\{\begin{array}{l}{y=kx+t}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$��ȥy�ã���1+4k2��x2+8ktx+4t2-4=0��
���ɡ���0⇒4k2+1��t2��
x1+x2=$\frac{-8kt}{1+4{k}^{2}}$��x1•x2=$\frac{4{t}^{2}-4}{1+4{k}^{2}}$������6�֣�
y1+y2=kx1+t+kx2+t=k��x1+x2��+2t=$\frac{2t}{1+4{k}^{2}}$��
y1•y2=��kx1+t������kx2+t��=k2x1x2+kt��x1+x2��+t2��
=k2��$\frac{4{t}^{2}-4}{1+4{k}^{2}}$+kt��$\frac{-8kt}{1+4{k}^{2}}$��+t2��
=$\frac{{t}^{2}-4{k}^{2}}{1+4{k}^{2}}$��
����ABΪֱ����Բ������ԭ�㣬����$\overrightarrow{OA}•\overrightarrow{OB}=0$⇒x1x2+y1y2=0��
��x1x2+y1y2=$\frac{4{t}^{2}-4}{1+4{k}^{2}}$+$\frac{{t}^{2}-4{k}^{2}}{1+4{k}^{2}}$=0��
��5t2=4+4k2������8�֣�
����0⇒4k2+1��t2��t��-$\frac{\sqrt{3}}{2}$��t��$\frac{\sqrt{3}}{2}$��
����AB���е�ΪD��m��n�������У�$\left\{\begin{array}{l}{m=\frac{{x}_{1}+{x}_{2}}{2}=-\frac{4kt}{1+4{k}^{2}}}\\{n=\frac{{y}_{1}+{y}_{2}}{2}=\frac{t}{1+4{k}^{2}}}\end{array}\right.$��
��ֱ��PD��ֱ��l��ֱ������${k}_{PD}=-\frac{1}{k}$=$\frac{-\frac{3}{2}-n}{-m}$⇒$\frac{t}{1+4{k}^{2}}$=$\frac{1}{2}$������10�֣�
��$\left\{\begin{array}{l}{\frac{t}{1+4{k}^{2}}=\frac{1}{2}}\\{5{t}^{2}=4+4{k}^{2}}\end{array}\right.$���$\left\{\begin{array}{l}{{t}_{1}=1}\\{{t}_{2}=-\frac{3}{5}}\end{array}\right.$��
��t=-$\frac{3}{5}$ʱ������0��ȥ
��t=1ʱ��k=��$\frac{1}{2}$��
������ֱ�߷���Ϊy=$\frac{1}{2}$x+1��y=-$\frac{1}{2}$x+1������12�֣�
���� ���⿼��ֱ�߷��̡���Բ���̼�ֱ������Բλ�ù�ϵ���������������������㣬�����������˼�룬����ѧ���ۺ�����֪ʶ�������������������ۺ���ǿ���������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����F1��F2�ֱ�����ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬��A���¶��㣬������C2��y=x2-1��x�ύ�ڵ�F1��F2����y�ύ�ڵ�B���ҵ�B���߶�OA���е㣬��NΪ��������C2��һ���㣬����N��������C2�����߽���ԲC1��P��Q���㣮
��ͼ����F1��F2�ֱ�����ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬��A���¶��㣬������C2��y=x2-1��x�ύ�ڵ�F1��F2����y�ύ�ڵ�B���ҵ�B���߶�OA���е㣬��NΪ��������C2��һ���㣬����N��������C2�����߽���ԲC1��P��Q���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{1}{2}$�����ҽ���F�Ҵ�ֱ��x���ֱ������ԲC�ཻ��M��N���㣬��|MN|=3��
��֪��ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{1}{2}$�����ҽ���F�Ҵ�ֱ��x���ֱ������ԲC�ཻ��M��N���㣬��|MN|=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60 | B�� | 90 | C�� | 150 | D�� | 120 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [k��-$\frac{��}{12}$��k��+$\frac{5��}{12}$]��k��Z�� | B�� | [k��-$\frac{7��}{12}$��k��-$\frac{��}{12}$]��k��Z�� | ||
| C�� | [$\frac{2k��}{3}$-$\frac{��}{18}$��$\frac{2k��}{3}$+$\frac{5��}{18}$]��k��Z�� | D�� | [$\frac{2k��}{3}$-$\frac{7��}{18}$��$\frac{2k��}{3}$-$\frac{��}{18}$]��k��Z�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ཻ | B�� | ���� | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
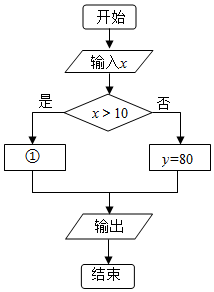 ij�������ֳ������ͧ���շѰ취���£�������ʮ�����շ�80Ԫ������ʮ���ӣ��������ְ�ÿ����10Ԫ�շѣ��������в���һ���ӵIJ��֣���С��0.5�������շѣ������ڻ����0.5������һ�����շѣ���С��ͬѧΪ�����ֳ������һ���շ������������ͼ��ͼ��ʾ������x�����ӣ�Ϊ����ʱ�䣬y��Ԫ��Ϊ���շ��ã���[x]��ʾ������x�������������ͼ�Тٴ�Ӧ�������
ij�������ֳ������ͧ���շѰ취���£�������ʮ�����շ�80Ԫ������ʮ���ӣ��������ְ�ÿ����10Ԫ�շѣ��������в���һ���ӵIJ��֣���С��0.5�������շѣ������ڻ����0.5������һ�����շѣ���С��ͬѧΪ�����ֳ������һ���շ������������ͼ��ͼ��ʾ������x�����ӣ�Ϊ����ʱ�䣬y��Ԫ��Ϊ���շ��ã���[x]��ʾ������x�������������ͼ�Тٴ�Ӧ�������| A�� | y=10[x] | B�� | y=10[x]-20 | C�� | y=10[x-$\frac{1}{2}$]-20 | D�� | y=10[x+$\frac{1}{2}$]-20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com