
已知二阶矩阵M有特征值 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 ,求矩阵M.
,求矩阵M.
科目:高中数学 来源: 题型:解答题
二阶矩阵M有特征值 ,其对应的一个特征向量e=
,其对应的一个特征向量e= ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成点
变换成点 .
.
(1)求矩阵M;
(2)求矩阵M的另一个特征值及对应的一个特征向量.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将正整数 (
( )任意排成
)任意排成 行
行 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若 表示某个
表示某个 行
行 列数表中第
列数表中第 行第
行第 列的数(
列的数( ,
,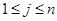 ),且满足
),且满足 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com