
二阶矩阵M有特征值 ,其对应的一个特征向量e=
,其对应的一个特征向量e= ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成点
变换成点 .
.
(1)求矩阵M;
(2)求矩阵M的另一个特征值及对应的一个特征向量.
(1)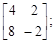 (2)
(2)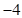 ,
,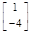
解析试题分析:(1)由于二阶矩阵M有特征值 ,其对应的一个特征向量e=
,其对应的一个特征向量e= ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成点
变换成点 .所以通过假设二阶矩阵,其中有四个变量,根据以上的条件特征值与特征向量,以及点通过矩阵的变换得到的点,可得到四个相应的方程,从而解得结论.
.所以通过假设二阶矩阵,其中有四个变量,根据以上的条件特征值与特征向量,以及点通过矩阵的变换得到的点,可得到四个相应的方程,从而解得结论.
(2)求矩阵M的特征值 ,根据特征多项式
,根据特征多项式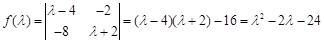 .即
.即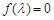 ,可求得
,可求得 的值,即可得另一个特征值.即可写出相应的一个特征向量.
的值,即可得另一个特征值.即可写出相应的一个特征向量.
试题解析:(1)解:(1)设M=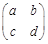 ,则由
,则由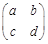
 =6
=6 得
得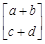 =
=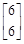 ,
,
即a+b=c+d=6.
由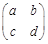
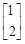 =
=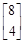 ,得
,得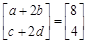 ,从而a+2b=8,c+2d=4.
,从而a+2b=8,c+2d=4.
由a+b =6及a+2b=8,解得a=4,b=2;
由c+d =6及c+2d=4,解得c=8,d=-2,
所以M=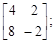
(2)由(1)知矩阵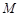 的特征多项式为
的特征多项式为
令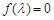 ,得矩阵
,得矩阵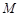 的特征值为6与
的特征值为6与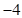 .
.
当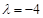 时,
时, 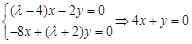
故矩阵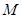 的属于另一个特征值
的属于另一个特征值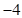 的一个特征向量为
的一个特征向量为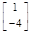 .
.
考点:1.矩阵的变换.2.特征向量特征值的求法.3.线性问题模型化.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com