
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2$\sqrt{2}$x |
分析 求出H的坐标,代入双曲线方程,然后转化求解a、b关系,即可得到结果.
解答 解:不妨设垂足H在第一象限,则由$\left\{{\begin{array}{l}{y=\frac{b}{a}x}\\{y=-\frac{a}{b}(x-c)}\end{array}}\right.$,得$H(\frac{a^2}{c},\frac{ab}{c})$,
故$M(\frac{1}{2}(\frac{a^2}{c}+c),\frac{ab}{2c})$,
把点M坐标代入双曲线方程中得$\frac{1}{4}{(\frac{a}{c}+\frac{c}{a})^2}-\frac{1}{4}{(\frac{a}{c})^2}=1$.
即有$\frac{c^2}{a^2}=2$,解得a=b,
故双曲线C的渐近线方程为y=±x.
点评 本题考查双曲线的简单性质的应用,直线与双曲线方程的位置关系,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
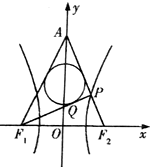 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com