分析:(Ⅰ)欲证FE∥面DD1C1C,根据直线与平面平行的判定定理可知只需证FE与面DD1C1C内一直线平行,连A1B,根据比例关系可知FE∥A1B,又D1C∥A1B,则EF∥D1C,EF?面DD1C1C,D1C?面DD1C1C,满足定理所需条件;
(Ⅱ)过点D作DG⊥EC,连接D1G,根据二面角平面角的定义可知∠D1GD就是二面角A-EC-D1的平面角,然后在△D1DG中求出此角的正切值即可求得所求.
解答:解:(Ⅰ)连A
1B,∵AE=3EB.
A1F=FA∴
==3,∴FE∥A
1B,又D
1C∥A
1B
∴EF∥D
1C,EF?面DD
1C
1C,D
1C?面DD
1C
1C
∴FE∥面DD
1C
1C
(Ⅱ)过点D作DG⊥EC,连接D
1G.
由DD
1⊥平面ABCD得D
1G⊥CE,又DG⊥EC,DG∩DD
1=D,
∴CE⊥平面D
1DG.∴CE⊥D
1G,
∴∠D
1GD就是二面角A-EC-D
1的平面角.
设正方体ABCD-A
1B
1C
1D
1的棱长为4,则AE=3,EB=1.
CE==,△DEC中,由等面积法,
DG==.
∴△D
1DG中,
tanD1GD===.
∴二面角A-EC-D
1的正切值为
点评:本题主要考查了线面平行的判定,以及二面角的度量,求二面角,关键是构造出二面角的平面角,同时考查了计算能力,属于中档题.

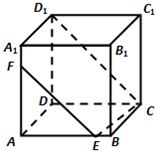


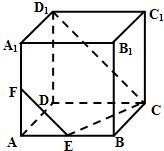 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )