Question

14．在平面直角坐标系中，O为坐标原点，从单位圆外一点A引圆O的两条切线，切点分别为B₁，B₂，若满足条件|$\overrightarrow{c}$-（$\overrightarrow{O{B}_{1}}$+$\overrightarrow{O{B}_{2}}$）|=|$\overrightarrow{O{B}_{1}}$-$\overrightarrow{O{B}_{2}}$|的向量$\overrightarrow{c}$的模最大时，则$\overrightarrow{A{B}_{1}}$•$\overrightarrow{A{B}_{2}}$=0．

Answer 1

分析 根据条件确定$\overrightarrow{c}$的终点的轨迹，寻找|$\overrightarrow{c}$|取得最大值时的条件，从而得出$\overrightarrow{A{B}_{1}}$•$\overrightarrow{A{B}_{2}}$的值．

解答 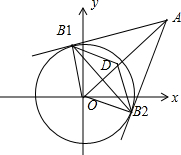解：设$\overrightarrow{O{B}_{1}}+\overrightarrow{O{B}_{2}}$=$\overrightarrow{OD}$，则D在线段OA上，设$\overrightarrow{OC}$=$\overrightarrow{c}$，
∵|$\overrightarrow{c}$-（$\overrightarrow{O{B}_{1}}$+$\overrightarrow{O{B}_{2}}$）|=|$\overrightarrow{O{B}_{1}}$-$\overrightarrow{O{B}_{2}}$|=|$\overrightarrow{{B}_{2}{B}_{1}}$|．
∴C的轨迹在以D为圆心，以|B₁B₂|为半径的圆上，
∴|$\overrightarrow{c}$|的最大值为|$\overrightarrow{OD}$|+|$\overrightarrow{{B}_{1}{B}_{2}}$|=|$\overrightarrow{O{B}_{1}}+\overrightarrow{O{B}_{2}}$|+|$\overrightarrow{O{B}_{1}}-\overrightarrow{O{B}_{2}}$|，
∴当|$\overrightarrow{O{B}_{1}}+\overrightarrow{O{B}_{2}}$|=|$\overrightarrow{O{B}_{1}}-\overrightarrow{O{B}_{2}}$|时，即$\overrightarrow{O{B}_{1}}$⊥$\overrightarrow{O{B}_{2}}$时，|$\overrightarrow{c}$|取得最大值．
此时，四边形AB₁OB₂为正方形，
∴$\overrightarrow{A{B}_{1}}•\overrightarrow{A{B}_{2}}=0$．
故答案为：0．

点评 本题考查了平面向量线性运算的几何意义，平面向量的数量积运算，属于中档题．