已知函数f(x)是定义在R上的奇函数，当x＜0时，f(x)＝ex(x＋1)，给出下列命题：
①当x＞0时，f(x)＝ex(1－x)；②函数f(x)有两个零点；③f(x)＞0的解集为(－1,0)∪(1，＋∞)；④?x1，x2∈R，都有|f(x1)－f(x2)|＜2.
其中正确命题的个数是( )
A．1 B．2
C．3 D．4
名校课堂系列答案科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷4练习卷（解析版） 题型：解答题
如图，已知四棱锥P－ABCD的底面为直角梯形，AB∥CD，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝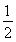
AB＝1，M是PB的中点．
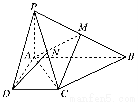
(1)求证：AM＝CM；
(2)若N是PC的中点，求证：DN∥平面AMC.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷2练习卷（解析版） 题型：解答题
已知△ABC的内角为A、B、C，其对边分别为a、b、c，B为锐角，向量m＝(2sin B，－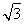
)，n＝
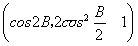，且m∥n
(1)求角B的大小；
(2)如果b＝2，求S△ABC的最大值．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：解答题
已知函数f(x)＝ax2－ln x，x∈(0，e]，其中e是自然对数的底数，a∈R.
(1)当a＝1时，求函数f(x)的单调区间与极值；
(2)是否存在实数a，使f(x)的最小值是3？若存在，求出a的值；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：填空题
已知集合A、B，定义集合A与B的一种运算A⊕B，其结果如下表所示：
A | {1,2,3,4} | {－1,1} | {－4,8} | {－1,0,1} |
B | {2,3,6} | {－1,1} | {－4，－2,0,2} | {－2，－1,0,1} |
A⊕B | {1,4,6} | ∅ | {－2,0,2,8} | {－2} |
按照上述定义，若M＝{－2 011,0,2 012}，N＝{－2 012,0,2 013}，则M⊕N＝________.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：选择题
若a，b∈R，且ab＞0，则下列不等式中，恒成立的是( )
A．a＋b≥2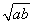
B.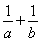
＞
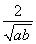
C.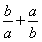
≥2 D．a2＋b2＞2ab
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练D组练习卷（解析版） 题型：解答题
如图，某园林单位准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余的地方种花，若BC＝a，∠ABC＝θ，设△ABC的面积为S1，正方形的PQRS面积为S2.
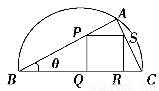
(1)用a，θ表示S1和S2；
(2)当a固定，θ变化时，求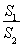
的最小值．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练A组练习卷（解析版） 题型：解答题
如图，已知椭圆C：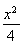
＋y2＝1，A、B是四条直线x＝±2，y＝±1所围成的两个顶点．
(1)设P是椭圆C上任意一点，若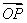
＝m
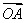＋n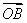
，求证：动点Q(m，n)在定圆上运动，并求出定圆的方程；
(2)若M、N是椭圆C上两上动点，且直线OM、ON的斜率之积等于直线OA、OB的斜率之积，试探求△OMN的面积是否为定值，说明理由．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练填空题押题练D组练习卷（解析版） 题型：填空题
设a＝2 0110.1，b＝ln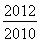
，c＝log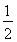
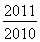，则a，b，c的大小关系是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
