
 如图所示的数阵是由非零自然数连续排列构成的,其中第n行中有n个数,则第n行所有数的和是$\frac{1}{2}$n(n2+1).
如图所示的数阵是由非零自然数连续排列构成的,其中第n行中有n个数,则第n行所有数的和是$\frac{1}{2}$n(n2+1). 分析 数阵的第n行有n个数,求得第n行最右边的数为$\frac{1}{2}$n(n+1),则第n行最左边的数为为$\frac{1}{2}$n(n+1)-(n-1),由等差数列的求和公式计算即可得到.
解答 解:数阵的第n行有n个数,前n行所有个数为:1+2+3+…+n=$\frac{1}{2}$n(n+1),
所以,第n行最右边的数为$\frac{1}{2}$n(n+1).
第n行最左边的数为$\frac{1}{2}$n(n+1)-(n-1)=$\frac{1}{2}$n2-$\frac{1}{2}$n+1,
即有第n行所有数的和是$\frac{1}{2}$n($\frac{1}{2}$n2-$\frac{1}{2}$n+1+$\frac{1}{2}$n(n+1))
=$\frac{1}{2}$n(n2+1).
故答案为:$\frac{1}{2}$n(n2+1).
点评 本题考查数列的应用,着重考查等差数列的求和公式的应用,突出考查观察问题、分析问题、解决问题的能力,考查学生数学的思维品质,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
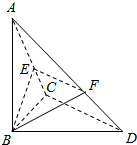 已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).
已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $±\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com