Question

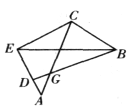
【题目】如图，线段、交于点，在的延长线上任取一点，得凸四边形，求证：、、的外接圆三圆共点。

Answer 1

【答案】见解析

【解析】

记与的外接圆分别为圆、圆，因为两圆已知有一个公共点，所以，两圆的位置或是相切或是相交。

（1）圆、圆相切。由于点在圆内部，因此，圆内切于圆，切点为，

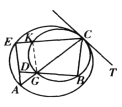
如图，记与圆交于，联结，过作两圆的公切线。由弦切角定理得

又由圆内接四边形对角互补得。

因此，.所以，、、、四点共圆。

这说明、、的外接圆三圆共点。

（2）圆、圆相交。记两圆的另一交点为，当为或时，就是三个外接圆的公共点；当既不是也不是时，分以下四种情况讨论。

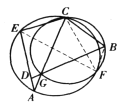
（i）如图，在之外，联结、、，则，所以，、、、四点共圆。这说明、、的外接圆三圆共点。

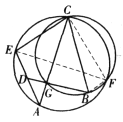
（ii）如图，在内，联结、、，则，又由圆内接四边形对角互补得。因此，，所以，、、、四点共圆，这说明、、的外接圆三圆共点。

（iii）如图，在之外，证明同（i）。

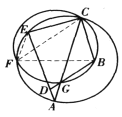
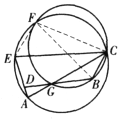
（iv）如图，在内，证明同（ii）。综上，、、的外接圆三圆共点。