
分析 ①根据一条直线与两个平行平面中的一个垂直,那么它与另一个平面垂直,即可判断正误;
②根据两个平面平行的判断方法即可判断正误;
③根据直线与平面平行的判断方法,得出命题错误;
④根据两个平面垂直的性质定理,即可判断命题错误.
解答 解:对于①,当α∥β时,若l⊥α,则l⊥β,
理由是如果一条直线与两个平行平面中的一个垂直,那么它与另一个平面垂直,∴①正确;
对于②,当l∥m,l?α,m?β时,α∥β或α与β相交,∴②错误;
对于③,当m⊥α,l⊥m时,l∥α或l?α,∴③错误;
对于④,当α⊥β,l?α,m?β时,l⊥m或l与m不垂直,∴④错误.
综上,正确的命题是①.
故答案为:①.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了几何符号语言与空间想象能力的应用问题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
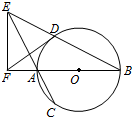 如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
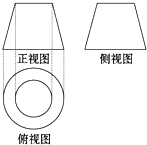 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )| A. | 6π | B. | 12π | C. | 18π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com