【题目】已知抛物线
的焦点为
，且过点
，椭圆
的离心率为
，点
为抛物线
与椭圆
的一个公共点，且
.
（1）求椭圆的方程；
（2）过椭圆内一点
的直线
的斜率为
，且与椭圆交于
两点，设直线
，
（
为坐标原点）的斜率分别为
，
，若对任意，存在实数
，使得
，求实数的取值范围.
【答案】（1）
（2）
【解析】试题分析：（1）由点
在抛物线
上，可求出抛物线
的方程为
，设
，则由抛物线的定义可得
，代入抛物线方程可解得
，
椭圆的离心率
，所以
，
又点在椭圆上，所以
，解得
，
，可得椭圆
的方程.
（2）设直线
的方程为
.联立消元可得
，
设
，
， 
，根据韦达定理，由
，得
，因为此等式对任意的
都成立，所以
，即
.
由题意得点
在椭圆内，可求实数
的取值范围.
试题解析：（1）由点在抛物线上，得
，解得
.
所以抛物线的方程为，其焦点
，
设，则由抛物线的定义可得
，解得，
代入抛物线方程可得
，解得
，所以，
椭圆的离心率，所以，
又点在椭圆上，所以，解得
，
，
所以椭圆的方程为.
（2）设直线的方程为.
由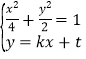
，消元可得，
设，，则
，
，
而
，由，得，
因为此等式对任意的都成立，所以，即.
由题意得点在椭圆内，故
，即
，解得.
科目：高中数学 来源： 题型：
【题目】已知在长方体ABCD-A1B1C1D1中，AB=2，BC=2，CC1=3，长方体每条棱所在直线与过点C1的平面α所成的角都相等，则直线AC与平面α所成角的余弦值为（ ）
A. 
或1 B. 或0 C. 
或0 D. 或1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是一个几何体的平面展开图，其中四边形ABCD为正方形，△PDC, △PBC, △PAB, △PDA为全等的等边三角形，E、F分别为PA、PD的中点，在此几何体中，下列结论中错误的为 （ ）
A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线
C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，
平面
，四边形是菱形，
，
，且
，
交于点
，
是
上任意一点．
（1）求证：
；
（2）若为的中点，且二面角
的余弦值为
，求
与平面
所成角
的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中，以坐标原点为极点，
轴的非负半轴为极轴建立极坐标系．已知点
的极坐标为
，直线
的极坐标方程为
，且点在直线上．
（1）求
的值及直线的直角坐标方程；
（2）圆
的极坐标方程为
，试判断直线与圆的位置关系．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学为弘扬优良传统，展示80年来的办学成果，特举办“建校80周年教育成果展示月”活动。现在需要招募活动开幕式的志愿者，在众多候选人中选取100名志愿者，为了在志愿者中选拔出节目主持人，现按身高分组，得到的频率分布表如图所示.
（1）请补充频率分布表中空白位置相应数据，再在答题纸上完成下列频率分布直方图；
（2）为选拔出主持人，决定在第3、4、5组中用分层抽样抽取6人上台，求第3、4、5组每组各抽取多少人？
（3）在（2）的前提下，主持人会在上台的6人中随机抽取2人表演诗歌朗诵，求第3组至少有一人被抽取的概率？
参考公式：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
:
的一个焦点与抛物线
的焦点重合，且过点
.过点
的直线
交椭圆
于
， 
两点， 
为椭圆的左顶点.
(Ⅰ)求椭圆
的标准方程；
(Ⅱ)求
面积的最大值，并求此时直线
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
