
空间中,对于平面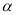 和共面的两直线
和共面的两直线 、
、 ,下列命题中为真命题的是( ).
,下列命题中为真命题的是( ).
A.若 ,
,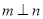 ,则
,则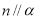
B.若 ,
,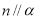 ,则
,则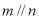
C.若 、
、 与
与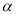 所成的角相等,则
所成的角相等,则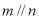
D.若 ,
, ,则
,则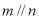
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试文科数学试卷(解析版) 题型:填空题
已知 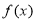 是定义在R上的奇函数,当
是定义在R上的奇函数,当 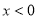 时
时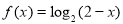 ,则
,则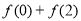 的值为_____.
的值为_____.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研文科数学试卷(解析版) 题型:填空题
 是平面内不共线的三点,点
是平面内不共线的三点,点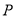 在该平面内且有
在该平面内且有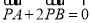 ,现将一粒黄豆随机
,现将一粒黄豆随机
撒在 内,则这粒黄豆落在
内,则这粒黄豆落在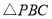 内的概率为___________.
内的概率为___________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研理科数学试卷(解析版) 题型:解答题
(本小题满分12分) 惠州市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为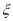 ,求
,求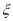 的分布列和数学期望;
的分布列和数学期望;
(2)已知第一次训练时用过的球放回后都当作旧球,求第二次训练时恰好取到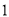 个新球的概率.
个新球的概率.
参考公式:互斥事件加法公式: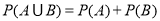 (事件
(事件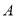 与事件
与事件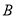 互斥).
互斥).
独立事件乘法公式: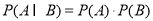 (事件
(事件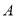 与事件
与事件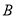 相互独立).
相互独立).
条件概率公式: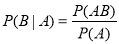 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)对于函数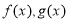 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数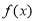 和
和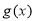 在点P处相切,称点P为这两个函数的切点. 设函数
在点P处相切,称点P为这两个函数的切点. 设函数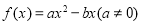 ,
,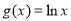 .
.
(Ⅰ)当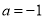 ,
,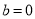 时, 判断函数
时, 判断函数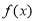 和
和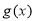 是否相切?并说明理由;
是否相切?并说明理由;
(Ⅱ)已知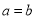 ,
,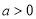 ,且函数
,且函数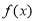 和
和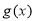 相切,求切点P的坐标;
相切,求切点P的坐标;
(Ⅲ)设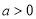 ,点P的坐标为
,点P的坐标为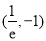 ,问是否存在符合条件的函数
,问是否存在符合条件的函数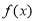 和
和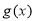 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为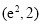 呢?(结论不要求证明)
呢?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试文科数学试卷(解析版) 题型:填空题
某小学教师准备购买一些签字笔和铅笔盒作为奖品,已知签字笔每支5元,铅笔盒每个6元,花费总额不能超过50元. 为了便于学生选择,购买签字笔和铅笔盒的个数均不能少于3个,那么该教师有_______种不同的购买奖品方案.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
现有两种投资方案,一年后投资盈亏的情况如下:
(1)投资股市:
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概 率 |
|
|
|
(2)购买基金:
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概 率 |
|
|
|
(Ⅰ)当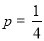 时,求q的值;
时,求q的值;
(Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于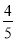 ,求
,求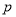 的取值范围;
的取值范围;
(Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知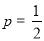 ,
,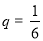 ,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.
,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研文科数学试卷(解析版) 题型:解答题
已知函数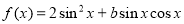 满足
满足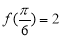
(1)求实数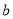 的值以及函数
的值以及函数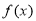 的最小正周期;
的最小正周期;
(2)记 ,若函数
,若函数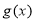 是偶函数,求实数
是偶函数,求实数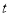 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com