
(本小题满分13分)对于函数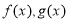 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数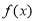 和
和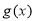 在点P处相切,称点P为这两个函数的切点. 设函数
在点P处相切,称点P为这两个函数的切点. 设函数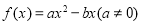 ,
,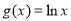 .
.
(Ⅰ)当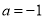 ,
,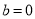 时, 判断函数
时, 判断函数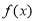 和
和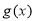 是否相切?并说明理由;
是否相切?并说明理由;
(Ⅱ)已知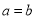 ,
,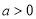 ,且函数
,且函数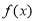 和
和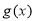 相切,求切点P的坐标;
相切,求切点P的坐标;
(Ⅲ)设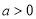 ,点P的坐标为
,点P的坐标为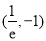 ,问是否存在符合条件的函数
,问是否存在符合条件的函数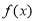 和
和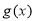 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为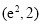 呢?(结论不要求证明)
呢?(结论不要求证明)
(Ⅰ)函数 和
和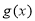 不相切.; (Ⅱ)
不相切.; (Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)由条件知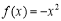 ,由
,由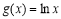 ,得
,得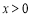 , 又因为
, 又因为 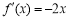 ,
,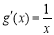 , 所以当
, 所以当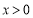 时,
时,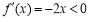 ,
, ,所以对于任意的
,所以对于任意的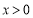 ,
,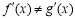 .即可证明,当
.即可证明,当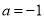 ,
,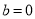 时,函数
时,函数 和
和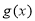 不相切. (Ⅱ)若
不相切. (Ⅱ)若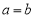 ,则
,则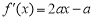 ,
,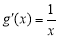 ,设切点坐标为
,设切点坐标为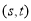 ,其中
,其中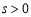 ,
,
由题意,得 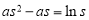 ①;
①;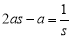 ② 可得
② 可得 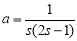 ,
,  ,进而的
,进而的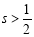 .
.
设函数 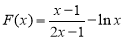 ,
,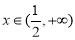 ,则
,则 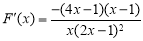 ,列出当
,列出当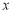 变化时,
变化时, 与
与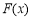 的变化情况表,可得切点P的坐标;(Ⅲ)由(Ⅰ)、(Ⅱ)即可得到结果.
的变化情况表,可得切点P的坐标;(Ⅲ)由(Ⅰ)、(Ⅱ)即可得到结果.
试题解析:(Ⅰ)【解析】
结论:当 ,
,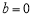 时,函数
时,函数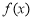 和
和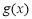 不相切. 1分
不相切. 1分
理由如下:
由条件知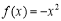 ,
,
由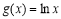 ,得
,得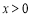 ,
,
又因为 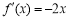 ,
,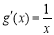 , 2分
, 2分
所以当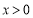 时,
时,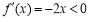 ,
, ,
,
所以对于任意的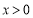 ,
,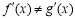 .
.
当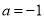 ,
,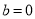 时,函数
时,函数 和
和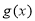 不相切. 3分
不相切. 3分
(Ⅱ)【解析】
若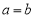 ,则
,则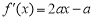 ,
,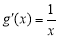 ,
,
设切点坐标为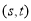 ,其中
,其中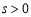 ,
,
由题意,得 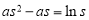 , ①
, ①
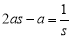 , ② 4分
, ② 4分
由②,得 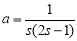 ,
,
代入①,得  . (*) 5分
. (*) 5分
因为 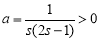 ,且
,且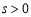 ,
,
所以 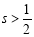 .
.
设函数 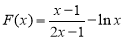 ,
,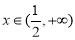 ,
,
则 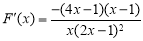 . 6分
. 6分
令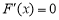 ,解得
,解得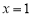 或
或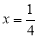 (舍). 7分
(舍). 7分
当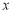 变化时,
变化时, 与
与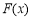 的变化情况如下表所示,
的变化情况如下表所示,
|
| 1 |
|
|
| 0 |
|
| ↗ | ↘ |
8分
所以当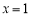 时,
时,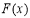 取到最大值
取到最大值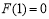 ,且当
,且当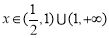 时
时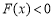 .
.
因此,当且仅当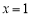 时
时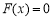 .
.
所以方程(*)有且仅有一解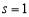 .
.
于是  ,
,
因此切点P的坐标为 . 9分
. 9分
(Ⅲ)【解析】
当点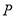 的坐标为
的坐标为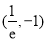 时,存在符合条件的函数
时,存在符合条件的函数 和
和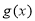 ,使得它们在点
,使得它们在点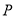
处相切; 11分
当点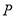 的坐标为
的坐标为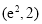 时,不存在符合条件的函数
时,不存在符合条件的函数 和
和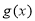 ,使得它们在点
,使得它们在点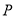 处相切. 13分.
处相切. 13分.
考点:1.导数的几何意义;2.导数在函数单调性上的应用.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试文科数学试卷(解析版) 题型:填空题
设复数z满足 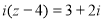 (i是虚数单位),则z的虚部为_______.
(i是虚数单位),则z的虚部为_______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研理科数学试卷(解析版) 题型:选择题
空间中,对于平面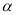 和共面的两直线
和共面的两直线 、
、 ,下列命题中为真命题的是( ).
,下列命题中为真命题的是( ).
A.若 ,
,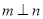 ,则
,则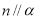
B.若 ,
,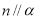 ,则
,则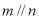
C.若 、
、 与
与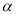 所成的角相等,则
所成的角相等,则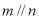
D.若 ,
, ,则
,则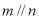
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数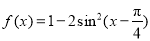 ,x∈R .
,x∈R .
(Ⅰ)求函数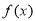 的最小正周期;
的最小正周期;
(Ⅱ)判断函数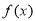 在区间
在区间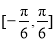 上是否为增函数?并说明理由.
上是否为增函数?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试文科数学试卷(解析版) 题型:选择题
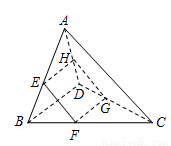
如图,在空间四边形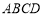 中,两条对角线
中,两条对角线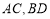 互相垂直,且长度分别为4和6,平行于这两条对角线的平面与边
互相垂直,且长度分别为4和6,平行于这两条对角线的平面与边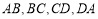 分别相交于点
分别相交于点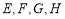 ,记四边形
,记四边形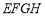 的面积为y,设
的面积为y,设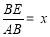 ,则( )
,则( )
(A)函数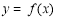 的值域为
的值域为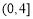
(B)函数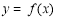 的最大值为8
的最大值为8
(C)函数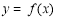 在
在 上单调递减
上单调递减
(D)函数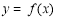 满足
满足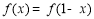
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么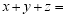 ______.
______.
|
| 3 |
| a |
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com